已知函数f(x)＝＋log₂

(1)判别函数的奇偶性，说明理由；

(2)解不等式f(x)－≤2

设h(x)＝，x∈[，5]，其中m是不等于零的常数，

(1)写出h(4x)的定义域；

(2)求h(x)的单调递增区间；

(3)已知函数f(x)(x∈[a，b])，定义：f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])．其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值．例如：f(x)＝cosx，x∈[0，π]，则f₁(x)＝cosx，x∈[0，π]，f₂(x)＝1，x∈[0，π]，当m＝1时，设，不等式t≤M₁(x)－M₂(x)≤n恒成立，求t，n的取值范围；

数列{a_n}的前n项和记为S_n，前kn项和记为S_kn(n，k∈N^*)，对给定的常数k，若是与n无关的非零常数t＝f(k)，则称该数列{a_n}是“k类和科比数列”，(1)、已知S_n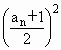＝，a_n＞0，求数列{a_n}的通项公式；

(2)证明(1)的数列{a_n}是一个“k类和科比数列”；

(3)设正数列{c_n}是一个等比数列，首项c₁，公比Q(Q≠1)，若数列{lgc_n}是一个“k类和科比数列”，探究c₁与Q的关系

已知是x，y轴正方向的单位向量，设＝(x＋2)＋y，＝(x＋2)＋y，＝(x－2)＋，且满足||－||＝2

(1)求点P(x，y)的轨迹E的方程．

(2)若直线l过点F₂(2，0)且法向量为＝(t，1)，直线与轨迹E交于P、Q两点．点M(－1，0)，无论直线l绕点F₂怎样转动，·是否为定值？如果是，求出定值；如果不是，请说明理由．并求实数t的取值范围；

在△ABC中，已知角A为锐角，且．

(1)将f(A)化简成f(A)＝Msin(wA＋φ)＋N的形式；

(2)若A＋B＝，f(A)＝1，BC＝2，求边AC的长．

已知函数

(1)判别函数的奇偶性，说明理由；

(2)解不等式

已知函数f(x)＝－x³＋ax²－4，(a∈R)，(x)是f(x)的导函数．

(Ⅰ)当a＝2时，对于任意的m∈[－1，1]，n∈[－1，1]，求f(m)＋(n)的最小值；

(Ⅱ)若存在x₀∈(0，＋∞)，使f(x₀＞0)，求a的取值范围．

已知椭圆C的中心为直角坐标系xOy的原点，焦点在x轴上，它在x轴上的一个顶点到两个焦点的距离分别是7和1．

(Ⅰ)求椭圆C的方程；

(Ⅱ)若P为椭圆C上的动点，M为过P且垂直于x轴的直线上的点，＝e(e为椭圆C的离心率)，求点M的轨迹方程，并说明轨迹是什么曲线．

已知四棱锥P－ABCD的三视图如图，该棱锥中，PA＝AB＝1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在棱BC上移动．

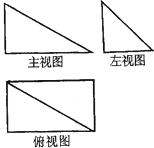
(Ⅰ)画出该棱锥的直观图并证明：无论点E在棱BC的何处，总有PE⊥AF；

(Ⅱ)连接DE，设G为DE上一动点，当三棱锥P－AGE的体积为时，试确定G在DE上的位置．

一人盒子中装有4张卡片，每张卡上写有1个数字，数字分别是0，1、2、3．现从盒子中随机抽取卡片．

(Ⅰ)若一次抽取3张卡片，求3张卡片上数字之和大于等于5的概率；

(Ⅱ)若第一次抽1张卡片，放回后再抽取1张卡片，求两次抽取中至少一次抽到数字2的概率．