济南高新区引进一高科技企业，投入资金720万元建设基本设施，第一年各种运营费用120万元，以后每年增加40万元；每年企业销售收入500万元，设f(n)表示前n年的纯收入．(f(n)＝前n年的总收入－前n年的总支出－投资额)

(Ⅰ)从第几年开始获取纯利润？

(Ⅱ)若干年后，该企业为开发新产品，有两种处理方案：

①年平均利润最大时，以480万元出售该企业；

②纯利润最大时，以160万元出售该企业；

问哪种方案最合算？

已知定义在实数集R上的奇函数f(x)有最小正周期2，且当x∈(0，1)时，f(x)＝

(Ⅰ)求函数f(x)在(－1，1)上的解析式；

(Ⅱ)判断f(x)在(0，1)上的单调性；

(Ⅲ)当λ取何值时，方程f(x)＝λ在(－1，1)上有实数解？

已知平面向量a＝(，－1)，b＝(，)

(Ⅰ)若存在实数k和t，满足x＝(t＋2)a＋(t²－t－5)b，y＝－ka＋4b且x⊥y，求出k关于t的关系式k＝f(t)；

(Ⅱ)根据(Ⅰ)的结论，试求出函数k＝f(t)在t∈(－2，2)上的最小值．

设函数y＝f(x)＝ax³＋bx²＋cx＋d的图象在x＝0处的切线方程为24x＋y－12＝0．

(Ⅰ)求c，d；

(Ⅱ)若函数在x＝2处取得极值－16，试求函数解析式并确定函数的单调区间．

已知{a_n}是一个公差大于0的等差数列，且满足a₃a₆＝55，a₂＋a₇＝16．

(Ⅰ)求数列{a_n}的通项公式：

(Ⅱ)等比数列{b_n}满足：b₁＝a₁，b₂＝a₂－1，若数列c_n＝a_n·b_n，求数列{c_n}的前n项和S_n．

在△ABC中，a、b、c分别为内角A、B、C的对边，且a²＝b²＋c²＋bc

(Ⅰ)求A的大小；

(Ⅱ)若sinB＋sinC＝1，试求内角B、C的大小．

设函数f(x)＝ln(x²＋ax＋1)的定义域为A．

(Ⅰ)若1∈A，－3A，求实数a的范围；

(Ⅱ)若函数y＝f(x)的定义域为R，求实数a的取值范围．

已知函数f(x)＝cosx－sinx＋1(x∈R)．

(Ⅰ)求函数y＝f(x)的最大值，并指出取得最大值时相应的x的值；

(Ⅱ)求函数y＝f(x)的单调增区间．

如图，已知椭圆C：＝1(a＞1)的上顶点为A，右焦点为F，直线AF与圆M：x²＋y²－6x－2y＋7＝0相切．

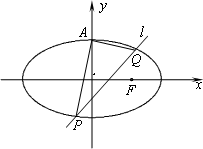
(Ⅰ)求椭圆C的方程；

(Ⅱ)若不过点A的动直线l与椭圆C相交于P、Q两点，且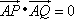求证：直线l过定点，并求出该定点N的坐标

已知数列{a_n}的前n项和为S_n，且S_n＝2a_n－2，(n＝1，2，3…)数列{b_n}中，b₁＝1，点P(b_n，b_n+1)在直线x－y＋2＝0上．

(Ⅰ)求数列{a_n}和{b_n}的通项公式；

(Ⅱ)记S_n＝a₁b₁＋a₂b₂＋…＋a_nb_n，求满足S_n＜167的最大正整数n．