椭圆过点P(1，)，其左、右焦点分别为F₁，F₂，离心率，M，N是直线x＝4上的两个动点，且

(1)求椭圆的方程；

(2)求|MN|的最小值；

(3)以MN为直径的圆C是否过定点？请证明你的结论．

某市环保研究所对市中心每天环境污染情况进行调查研究后，发现一天中环境综合污染指数f(x)与时间x(小时)的关系为，其中a是与气象有关的参数，且，若用每天f(x)的最大值为当天的综合污染指数，并记作M(a)．

(1)令，求t的取值范围；

(2)求函数M(a)；

(3)市政府规定，每天的综合污染指数不得超过2，试问目前市中心的综合污染是否超标？请说明理由．

如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．

(1)求证：AF∥平面BCE；

(2)求直线BF和平面BCE所成角的正弦值．

已知函数f(x)＝·，其中，相邻两对称轴间的距离不小于

(1)求的取值范围；

(2)在的面积．

已知△ABC的面积其中a，b，c分别为角A，B，C所对的边．

(1)求角A的大小；

(2)若a＝2，求的最大值．

已知点P_n(a_n，b_n)(n∈N^*)满足a_n+1＝a_nb_n+1，，且点P₁的坐标为(1，－1)．

(Ⅰ)求经过点P₁，P₂的直线l的方程；

(Ⅱ)已知点P_na(a_n，b_n)(n∈N^*)在P₁，P₂两点确定的直线l上，求数列{a_n}通项公式．

(Ⅲ)在(Ⅱ)的条件下，求对于所有n∈N^*，能使不等式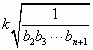成立的最大实数k的值．

某市公租房的房源位于A，B，C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的求该市的任4位申请人中：

(Ⅰ)恰有2人申请A片区房源的概率；

(Ⅱ)申请的房源所在片区的个数ξ的分布列与期望

已知(x＋1)ⁿ＝a₀＋a₁(x－1)＋a₂(x－1)²＋a₃(x－1)³＋…＋a_n(x－1)ⁿ，(其中n∈N^*)

(1)求a₀及S_n＝a₁＋a₂＋a₃＋…＋a_n；

(2)试比较S_n与(n－2)2ⁿ＋2n²的大小，并说明理由．

选修4－5：不等式选讲

若正数a，b，c满足a＋b＋c＝1，求的最小值．

选修4－4：坐标系与参数方程

椭圆中心在原点，焦点在x轴上．离心率为，点P(x，y)是椭圆上的一个动点，若的最大值为10，求椭圆的标准方程．