已知函数f(x)＝x³＋bx²＋cx＋d有两个极值点x₁＝1，x₂＝2，且直线y＝6x＋1与曲线y＝f(x)相切于P点．

(1)求b和c

(2)求函数y＝f(x)的解析式；

(3)在d为整数时，求过P点和y＝f(x)相切于一异于P点的直线方程

已知椭圆E的长轴的一个端点是抛物线y²＝4x的焦点，离心率是

(1)求椭圆E的方程；

(2)过点C(－1，0)，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使为常数？若存在，求出点M的坐标；若不存在，请说明理由．

某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，这两族人数占各自小区总人数的比例如下：

(1)从A，B，C三个社区中各选一人，求恰好有2人是低碳族的概率；

(2)在B小区中随机选择20户，从中抽取的3户中“非低碳族”数量为X，求X的分布列和期望EX．

如图，在四棱柱ABCD－A₁B₁C₁D₁中，侧面ADD₁A₁⊥底面ABCD，D₁A＝D₁D＝，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD＝2AB＝2BC＝2，O为AD中点．

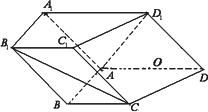
(Ⅰ)求证：A₁O∥平面AB₁C；

(Ⅱ)求锐二面角A－C₁D₁－C的余弦值．

设数列{b_n}的前n项和为S_n，且b_n＝2－2S_n；数列{a_n}为等差数列，且a₅＝14，a₇＝20．

(1)求数列{b_n}的通项公式；

(2)若c_n＝a_n·b_n(n＝1，2，3…)，T_n为数列{c_n}的前n项和．求T_n．

已知f(x)＝sin(2x－)＋2cos²x－1

(Ⅰ)求函数f(x)的单调增区间

(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，且a＝1，b＋c＝2，f(A)＝，求△ABC的面积．

已知椭圆E的长轴的一个端点是抛物线y²＝4x的焦点，离心率是

(1)求椭圆E的方程；

(2)过点C(－1，0)，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使·为常数？若存在，求出点M的坐标；若不存在，请说明理由．

定义在R上的函数f(x)＝ax³＋bx²＋cx＋3同时满足以下条件：

①f(x)在(0，1)上是减函数，在(1，＋∞)上是增函数；

②(x)是偶函数；

③f(x)在x＝0处的切线与直线y＝x＋2垂直．

(Ⅰ)求函数y＝f(x)的解析式；

(Ⅱ)设g(x)＝4lnx－m，若存在x∈[1，e]，使g(x)＜(x)，求实数m的取值范围．

某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周(阴影部分)为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同)，塑胶运动场地占地面积为S平方米．

(1)分别写出用x表示y和用x表示S的函数关系式(写出函数定义域)；

(2)怎样设计能使S取得最大值，最大值为多少？

如图所示，平面PAD⊥平面ABCD，ABCD为正方形，PA⊥AD，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点．

(1)求证：BC∥平面EFG；

(2)求三棱锥E－AFG的体积．