科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
已知圆M：
及定点
，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
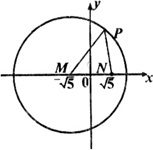
(1)求点G的轨迹C的方程；
(2)过点K(2，0)作直线l，与曲线C交于A、B两点，O是坐标原点，设
是否存在这样的直线l，使四边形OASB的对角线相等？若存在，求出直线l，的方程；若不存在，说明理由．
查看答案和解析>>
科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
已知函数f(x)是定义在实数集R上的奇函数，当x＞0时，
(1)已知函数f(x)的解析式；
(2)若函数f(x)在区间(－∞，－1)上是单调减函数，求a的取值范围；
(3)试证明对
．
查看答案和解析>>
科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定(平面图如图所示)，如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米2，水池所有墙的厚度忽略不计．
(1)试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
(2)若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低．
查看答案和解析>>
科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
如图，已知三棱锥P＝ABC中，PA⊥PC，D为AB的中点，M为PB的中点，且AB＝2PD．
(1)求证：DM∥面PAC；
(2)找出三棱锥P－ABC中一组面与面垂直的位置关系，并给出证明(只需找到一组即可)．
查看答案和解析>>
科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
已知{an}是公差为正数的等差数列，首项a1＝3，前n项和为Sn，数列{bn}是等比数列，首项
(1)求
的通项公式．
(2)令
的前n项和Tn．
查看答案和解析>>
科目： 来源：山东省烟台市2012届高三上学期期末考试数学文科试题 题型：044
已知函数
(1)求函数f(x)的最小正周期及单调递增区间；
(2)△ABC内角A、B、C的对边长分别为a、b、c，若
查看答案和解析>>
科目： 来源：北京市朝阳区2012届高三上学期期末考试数学理科试题 题型：044
数列{an}，{bn}(n＝1，2，3…)由下列条件确定：①a1＜0，b1＞0；②当k≥2时，ak与bk满足：当ak－1＋bk－1≥0时，ak＝ak－1，bk＝
；当ak－1＋bk－1＜0时，ak＝
，bk＝bk－1．
(Ⅰ)若a1＝－1，b1＝1，写出a2，a3，a4，并求数列{an}的通项公式；
(Ⅱ)在数列{bn}中，若b1＞b2＞…bs(s≥3，且s∈N*)，试用a1，b1表示bkk∈{1，2，…，s}；
(Ⅲ)在(Ⅰ)的条件下，设数列{cn}(n∈N*)满足c1＝
，cn≠0，cn+1＝－
(其中m为给定的不小于2的整数)，求证：当n≤m时，恒有cn＜1．
查看答案和解析>>
科目： 来源：北京市朝阳区2012届高三上学期期末考试数学理科试题 题型：044
已知椭圆C：
＝1(a＞b＞0)的离心率为
，直线l过点A(4，0)，B(0，2)，且与椭圆C相切于点P．
(Ⅰ)求椭圆C的方程；
(Ⅱ)是否存在过点A(4，0)的直线m与椭圆C相交于不同的两点M、N，使得36|AP|2＝35|AM|·|AN|？若存在，试求出直线m的方程；若不存在，请说明理由．
查看答案和解析>>
科目： 来源：北京市朝阳区2012届高三上学期期末考试数学理科试题 题型：044
已知函数f(x)＝ln(ax＋1)＋
(x≥0，a为正实数)．
(Ⅰ)若a＝1，求曲线y＝f(x)在点(1，f(1))处的切线方程；
(Ⅱ)求函数f(x)的单调区间；
(Ⅲ)若函数f(x)的最小值为1，求a的取值范围．
查看答案和解析>>
科目： 来源：北京市朝阳区2012届高三上学期期末考试数学理科试题 题型：044
如图，在四棱锥S－ABCD中，平面SAD⊥平面ABCD．底面ABCD为矩形，AD＝
a，AB＝
a，SA＝SD＝a．
(Ⅰ)求证：CD⊥SA；
(Ⅱ)求二面角C－SA－D的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com