解答题：解答应写出文字说明，证明过程或演算步骤

已知二次函数f(x)＝ax²＋bx＋1(a＞0，b∈R)设方程f(x)＝x有两个实数根x₁、x₂．

(1)

(2)

解答题

已知二次函数f(x)＝ax²＋bx＋c，满足f(0)＝f(x)＝0，且f(x)的最小值是．

(1)

(2)

(3)

解答题:解答应写出文字说明，证明过程或演算步骤．

如图，过抛物线x²＝4y的对称轴上任一点P(0，m)(m>0)作直线与抛物线交于A、B两点，点Q是点P关于原点的对称点．

(1)

(2)

解答题:解答应写出文字说明，证明过程或演算步骤．

如图，已知棱柱ABCD－A₁B₁C₁D₁的底面是菱形，且AA1⊥面ABCD，，AD＝AA₁，F为棱AA₁的中点，M为线段BD₁的中点，

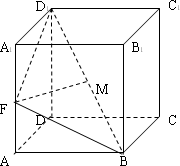
(1)

(2)

(3)

解答题：解答应写出文字说明，证明过程或演算步骤．

已知定义域为[0，1]的函数f(x)同时满足：

①对于任意的x[0，1]，总有f(x)≥0;

②f(1)＝1;

③若0≤x₁≤1，0≤x₂≤1，x₁＋x₂≤1，则有f(x₁＋x₂)≥f(x₁)＋f(x₂)．

(1)

(2)

(3)

解答题：解答应写出文字说明，证明过程或演算步骤

如图，在梯形ABCD中，AB∥CD，∠ADC＝90°，3AD＝DC＝3，AB＝2，E是DC上一点，满足DE＝1，连接AE，将△DAE沿AE折起到△D₁AE的位置，使得∠D₁AB＝60°，设AC与BE的交点．

(1)

(2)

(3)

设函数f(x)＝－4x＋b，不等式|f(x)|＜c的解集为(－1，2)

(1)

(2)

简答题

如图，点A、B分别是椭圆的长轴的左、右端点，F为椭圆的右焦点，直线PF的方程为且PA⊥PF．

(1)

(2)

简答题

如图，在三棱锥P－ABC中，PB⊥平面ABC，BE⊥平面PAC，PB＝AB＝2，

BC＝

(1)

(2)

解答题

已知f(x)是定义在实数集R上的增函数，设F(x)＝f(x)―f(a―x)．

(1)

(2)

(3)