已知S_n为数列{a_n}的前n项和，且S_n＝2a_n＋n²－3n－2，n＝1，2，3…

(1)求证：数列{a_n－2n}为等比数列；

(2)设b_n＝a_ncosnπ，求数列{b_n}的前n项和P_n；

(3)设，数列{C_n}的前n项和为T_n，，求证：T_n＜．

设二次函数f(x)＝x²＋bx＋c(b，c∈R)，已知不论α、β为何实数恒有f(sinα)≥0和f(2＋cosβ)≤0．

(1)求证：b＋c＝－1；

(2)求证c≥3；

(3)若函数f(sinα)的最大值为8，求b，c的值．

某建筑的金属支架如图所示，根据要求，AB的长至少为2.8 m，C为AB的中点，B到D的距离比CD的长小0.5 m，∠BCD＝60°，已知建筑支架的材料每米的价格一定，问如何设计AB、CD的长，可使建造这个支架的成本最低？

已知直线l₁：mx－y＝0，l₂：x＋my－m－2＝0．

(1)求证：对m∈R，l₁与l₂的交点P在一个定圆上；

(2)若l₁与定圆的另一个交点为P₁，l₂与定圆的另一交点为P₂，求当m在实数范围内取值时，ΔPP₁P₂面积的最大值及对应的m．

已知数列{a_n}的首项，，n＝1，2，…．

(Ⅰ)求{a_n}的通项公式；

(Ⅱ)证明：对任意的x＞0，，n＝1，2…；

(Ⅲ)证明：．

如下图，α和β为平面，α∩β＝l，A∈α，B∈β，AB＝5，A，B在棱l上的射影分别为，，A＝3，B＝2．若二面角α―l―β的大小为，求：

(Ⅰ)点B到平面α的距离；

(Ⅱ)异面直线l与AB所成的角(用反三角函数表示)．

如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC，，G，H分别为FA，FD的中点

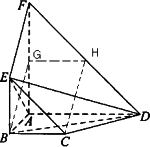
(Ⅰ)证明：四边形BCHG是平行四边形；

(Ⅱ)C，D，F，E四点是否共面？为什么？

(Ⅲ)设AB＝BE，证明：平面ADE⊥平面CDE；

已知z是实系数方程x²＋2bx＋c＝0的虚根，记它在直角坐标平面上的对应点为P_z(Rez，Imz)．

(1)若(b，c)在直线2x＋y＝0上，求证：P_z在圆C₁：(x－1)²＋y²＝1上；

(2)给定圆C：(x－m)²＋y²＝r²(m、r∈R，r＞0)，则存在唯一的线段s满足：①若P_z在圆C上，则(b，c)在线段s上；②若(b，c)是线段s上一点(非端点)，则P_z在圆C上．写出线段s的表达式，并说明理由；

(3)由(2)知线段s与圆C之间确定了一种对应关系，通过这种对应关系的研究，填写下表(表中s₁是(1)中圆C₁的对应线段)．

已知二面角α－CD－β的大小为60°，EA⊥平面α，垂足为A，EB⊥平面β，垂足为B，EA＝3，EB＝4．

(1)求证：CD⊥AB；

(2)求E到CD的距离．

如图，已知平面，ABCD为矩形，P∈B，PA⊥α，且PA＝AD，M、N、F依次是AB、PC、PD的中点．

(1)求证：四边形AMNF为平行四边形；

(2)求证：MN⊥AB

(3)求异面直线PA与MN所成角的大小．