
科目: 来源:大纲版2012届高三上学期单元测试(9)数学试题 题型:044
已知斜三棱柱ABC-A1B1C1中,A1C1=B1C1=2,D、D1分别是AB、A1B1的中点,平面A1ABB1⊥平面A1B1C1,异面直线AB1与C1B互相垂直.
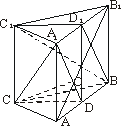
(1)求证:AB1⊥C1D1;
(2)求证:AB1⊥面A1CD;
(3)若AB1=3,求直线AC与平面A1CD所成的角.
查看答案和解析>>
科目: 来源:大纲版2012届高三上学期单元测试(9)数学试题 题型:044
如图所示,在平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.

(1)求证:AB⊥平面BCD;
(2)求点C到ABD的距离.
查看答案和解析>>
科目: 来源:大纲版2012届高三上学期单元测试(9)数学试题 题型:044
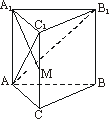
如图所示,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=![]() ,M是CC1的中点.求证:AB1⊥A1M.
,M是CC1的中点.求证:AB1⊥A1M.
查看答案和解析>>
科目: 来源:重庆市万州二中2012届高三10月月考数学理科试题 题型:044
已知函数f(x)=ax3+bx2+cx+d(x∈R,a≠0),-2是f(x)的一个零点,又f(x)在x=0处有极值,在区间(-6,-4)和(-2,0)上是单调的,且在这两个区间上的单调性相反.
(1)求![]() 的取值范围;
的取值范围;
(2)当b=3a时,求使{y|y=f(x),-3≤x≤2}![]() [-3,2]成立的实数a的取值范围.
[-3,2]成立的实数a的取值范围.
查看答案和解析>>
科目: 来源:重庆市万州二中2012届高三10月月考数学理科试题 题型:044
某企业生产甲、乙两种产品,根据市场调查与预测,甲产品的利润与投资成正比,其关系如图1,乙产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资的单位:万元).
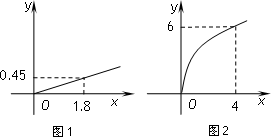
(Ⅰ)分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ)该企业筹集了100万元资金投入生产甲、乙两种产品,问:怎样分配这100万元资金,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目: 来源:重庆市万州二中2012届高三10月月考数学文科试题 题型:044
已知函数f(x)=ax3+bx2+cx+d(x∈R,a≠0),-2是f(x)的一个零点,又f(x)在x=0处有极值,在区间(-6,-4)和(-2,0)上是单调的,且在这两个区间上的单调性相反.
(1)求![]() 的取值范围;
的取值范围;
(2)当b=3a时,求使{y|y=f(x),-3≤x≤2}![]() [-3,2]成立的实数a的取值范围.
[-3,2]成立的实数a的取值范围.
查看答案和解析>>
科目: 来源:重庆市万州二中2012届高三10月月考数学文科试题 题型:044
某企业生产甲、乙两种产品,根据市场调查与预测,甲产品的利润与投资成正比,其关系如图1,乙产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资的单位:万元).
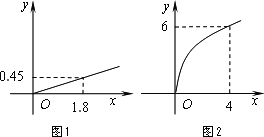
(1)分别将甲、乙两种产品的利润表示为投资的函数关系式;
(2)该企业筹集了100万元资金投入生产甲、乙两种产品,问:怎样分配这100万元资金,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目: 来源:福建省厦门外国语学校2012届高三10月月考数学文科试题 题型:044
已知函数![]() .
.
(Ⅰ)当m=时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当m=1时,证明方程f(x)=g(x)有且仅有一个实数根;
(Ⅲ)若x∈(1,e]时,不等式f(x)-g(x)<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源:福建省厦门外国语学校2012届高三10月月考数学文科试题 题型:044
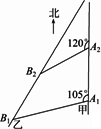
如图,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里.问乙船每小时航行多少海里?
海里.问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com