某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30．第6小组的频率是7．

(Ⅰ)求这次铅球测试成绩合格的人数；

(Ⅱ)若由直方图来估计这组数据的中位数，指出它在第几组内，并说明理由；

(Ⅲ)现在要从第6小组的学生中，随机选出2人参加“毕业运动会”，已知该组a、b的成绩均很优秀，求两人至少有1人入选的概率．

已知二次函数g(x)的图像经过坐标原点，且满足g(x＋1)＝g(x)＋2x＋1，设函数f(x)＝m[g(x＋1)－1]－lnx，其中m为常数且m＜0．

(1)求函数g(x)的解析式；

(2)判断函数f(x)的单调性并说明理由．

国家加大水利工程建设．某地区要修建一条灌溉水渠，其横断面为等腰梯形(如图)，底角A＝60°，考虑到坚固性及用料，要求横断面的面积为6m²，记水渠深为x m，用料部分的周长(即渠底BC及两腰长的和)为y m．

(1)求y关于x的函数关系式，并求定义域；

(2)当水渠的深x为多少m时，且x∈[3，2]时，横断面用料部分的周长最小？最小值是多少米？

如图，在四棱锥O－ABCD中，底面ABCD是边长为1的菱形，，OA⊥底面ABCD，OA＝2，M为OA的中点．

(1)求异面直线AB与MD所成角的大小；

(2)求平面OAB与平面OCD所成的二面角的余弦值．

已知数列a，b，c为各项都是正数的等差数列，公差为d(d＞0)，在a，b之间和b，c之间共插入m个实数后，所得到的m＋3个数所组成的数列{a_n}是等比数列，其公比为q．

(1)若a＝1，m＝1，求公差d；

(2)若在a，b之间和b，c之间所插入数的个数均为奇数，求所插入的m数的乘积(用a，c，m表示)

(3)求证：q是无理数．

已知f(x)＝ax－ln(－x)，x∈(－e，0)，g(x)＝－，其中e是自然常数，a∈R．

(1)讨论a＝－1时，f(x)的单调性、极值；

(2)求证：在(1)的条件下，|f(x)|＞g(x)＋；

(3)是否存在实数a，使f(x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．

已知椭圆C：＋y²＝1，过点(m，0)作圆x²＋y²＝1的切线l交椭圆G于A、B两点．

(1)求椭圆C的焦点坐标和离心率；

(2)将|AB|表示为m的函数，并求|AB|的最大值．

请你设计一个包装盒，如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE＝FB＝x cm．

(1)若广告商要求包装盒侧面积S(cm²)最大，试问x应取何值？

(2)若广告商要求包装盒容积V(cm³)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．

如图所示，在斜边为AB的Rt△ABC中，过A作PA⊥平面ABC，AM⊥PB于点M，AN⊥PC于点N．

(1)求证：BC⊥面PAC；

(2)求证：PB⊥面AMN；

(3)若PA＝AB＝4，设∠BPC＝，试用tan表示△AMN的面积，当tan取何值时，△AMN的面积最大？最大面积是多少？

如图，已知长方体ABCD－A₁B₁C₁D₁中，AB₁＝2，AA₁＝AD＝1，求：

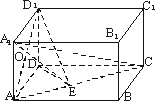
(1)点D₁到直线AC的距离；

(2)直线AB与面A₁DC的距离；

(3)异面直线A₁D与B₁C₁的距离．