已知函数f(x)＝ax＋xln|x＋b|是奇函数，且图像在点(e，f(e))(e为自然对数的底数)处的切线斜率为3．

(1)求实数a、b的值；

(2)若k∈Z，且k＜对任意x＞1恒成立，求k的最大值；

(3)当n＞m＞1，(n，m∈Z)时，证明：(mnⁿ)^m＞(nm^m)ⁿ．

已知函数f(x)＝px³＋qx²＋r，(p＞0)图象的对称中心为(1，0)，且f(x)的极小值为－2．

(1)求f(x)的解析式；

(2)设T(x)＝f(x)＋m，若T(x)有三个零点，求实数m的取值范围；

(3)是否存在实数k，当a＋b≤2时，使函数g(x)＝(x)＋k

在定义域[a，b]上的值域恰为[a，b]，若存在，求出k的范围；若不存在，说明理由．

数列{a_n}的前n项和为S_n，已知

(1)证明：数列是等差数列，并求S_n；

(2)设，求证：b₁＋b₂＋…＋b_n＜1．

(如图)半径为1，圆心角为120°的扇形，点P是扇形AB弧上的动点，设∠POA＝x．

(1)用x表示平行四边形ODPC的面积S＝f(x)；

(2)求平行四边形ODPC面积的最大值．

设集合A＝{x|≤2^－x≤4}，B＝{x|x²－3mx＋2m²－m－1＜0}．

(1)当x∈Z时，求A的非空真子集的个数；

(2)若，求实数m的取值范围．

已知函数f(x)定义在区间(－1，1)上，f()＝－1，对任意x，y∈(－1，1)，恒有成立，又数列{a_n}满足

(Ⅰ)在(－1，1)内求一个实数t，使得

(Ⅱ)求证：数列{f(a_n)}是等比数列，并求f(a_n)的表达式；

(Ⅲ)设，是否存在m∈N^*，使得对任意n∈N^*，恒成立？若存在，求出m的最小值；若不存在，请说明理由．

已知椭圆C的中心在圆点，焦点在x轴上，F₁，F₂分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F₁的直线l与椭圆交于A，B两点，△MF₁F₁的面积为4，△ABF₂的周长为8．

(Ⅰ)求椭圆C的方程；

(Ⅱ)设点Q的坐标为(1，0)，是否存在椭圆上的点P及以Q为圆心的一个圆，使得该圆与直线PF₁，PF₂都相切，若存在，求出P点坐标及圆的方程；若不存在，请说明理由．

如图所示，已知△AOB中，AB＝2OB＝4，D为AB的中点，若△AOC是△AOB绕直线AO旋转而成的，记二面角B－AO－C的大小为．

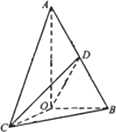
(Ⅰ)若＝，求证：平面COD⊥平面AOB；

(Ⅱ)若∈[，]时，求二面角C－OD－B的余弦值的最小值．

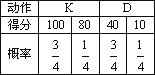
2010年广东亚运会，某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作，比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩．假设每个运动员完成每个系列中的两个动作的得分是相互独立的，根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：

　　甲系列：

　　乙系列：

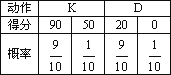
现该运动员最后一个出场，其之前运动员的最高得分为118分．

(Ⅰ)若该运动员希望获得该项目的第一名，应选择哪个系列，说明理由，并求其获得第一名的概率；

(Ⅱ)若该运动员选择乙系列，求其成绩X的分布列及其数学期望EX．

已知函数f(x)＝xlnx．

(Ⅰ)求函数f(x)在[t，t＋2](t＞0)上的最小值；

(Ⅱ)求证：对一切x∈(0，＋∞)，都有