设函数f(x)＝msinx＋cosx(x∈R)的图象经过点(，1)．

(1)求y＝f(x)的解析式，并求函数的最小正周期和最值；

(2)若f()＝sinA，其中A是面积为的锐角△ABC的内角，且AB＝2，求边AC和BC的长．

已知等差数列{a_n}的首项a₁＝19，且a₂＋a₃＝32，S_n为{a_n}的前n项和．

(1)求等差数列{a_n}通项公式a_n及前n项和S_n．

(2)设{b_n－a_n}是首项为1，公比为3的等比数列，求数列{b_n}的通项公式b_n及其前n项和T_n．

若函数f(x)＝2sin²ax－2sinax·cosax(a＞0)的图象与直线y＝m相切，并且切点的横坐标依次成公差为的等差数列．

(1)求m和a的值；

(2)设函数f(x)的最小正周期为T，设点P₁(x₁，y₁)，P₂(x₂，y₂)，…，P_n(x_n，y_n)(n∈N^*)在函数f(x)的图象上，且满足条件：x₁＝，x_n+1－x_n＝，求S_n＝y₁＋y₂＋…＋y₁₀的值．

我们用部分自然数构造如下的数表：用a_ij(i≥j)表示第i行第j个数(i、j为正整数)，使a_ij＝a_ii＝i；每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外，如图)，设第n(n为正整数)行中各数之和为b_n．

(1)试写出的关系(无需证明)；

(2)证明数列{b_n＋2}是等比数列，并求数列{b_n}的通项公式b_n．

已知等差数列{a_n}的首项为a，公差为b，且不等式ax²－3x＋2＞0的解集为(－∞，1)∪(b，＋∞)．

(1)求数列{a_n}的通项公式及前n项和S_n；

(2)比较的大小．

已知向量，且A，B，C分别是锐角三角形ABC三边a，b，c所对的角．

(1)求∠C的大小；

(2)若a，c，b成等比数列，且，求c的值．

某企业生产A、B两种产品，生产每一吨产品所需的劳动力、煤和电耗如下表：

已知生产每吨A产品的利润是7万元，生产每吨B产品的利润是12万元，现因条件限制，该企业仅有劳动力300个，煤360吨，并且供电局只能供电200千瓦，试问该企业生产A、B两种产品各多少吨，才能获得最大利润？

设{a_n}是一个公差为d(d≠0)的等差数列，它的前10项和S₁₀＝110且a₁，a₂，a₄成等比数列．

(1)证明a₁＝d；

(2)求公差d的值和数列{a_n}的通项公式．

已知函数f(x)＝alnx－(x－1)²－ax(常数a∈R)．

(Ⅰ)求f(x)的单调区间；

(Ⅱ)设a＞0．如果对于f(x)的图象上两点，存在x₀∈(x₁，x₂)，使得f(x)的图象在x＝x₀处的切线m∥P₁P₂，求证：．

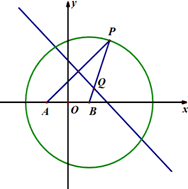
如图，已知点A(－2，0)，点P是⊙B：(x－2)²＋y²＝36上任意一点，线段AP的垂直平分线交BP于点Q，点Q的轨迹记为曲线C．

(Ⅰ)求曲线C的方程；

(Ⅱ)已知⊙O：x²＋y²＝r²(r＞0)的切线l总与曲线C有两个交点M、N，并且其中一条切线满足，求证：对于任意一条切线l总有．