已知，f(x)＝lnx，g(x)＝ax²＋3x＋1，(其中e为自然对数的底数)．

(Ⅰ)若函数h(x)＝f(x)－g(x)存在单调递减区间，求实数a的取值范围；

(Ⅱ)当0＜α＜β时，求证：αf(α)＋βf(β)＞(α＋β)f()；

(Ⅲ)证明当n＞2，n∈N^*时，log₂e＋log₃e＋log₄e＋…＋log_ne＞

已知函数f(x)＝x(x－a)＋2lnx＋1(a∈R)．

(1)当a＝5时，求函数f(x)的极值_；

(2)若不等式f(x)≥2－a对任意x∈[1，＋∞)恒成立，求实数a的取值范围．

己知等比数列的各项均为正数，且2a₁＋3a₂＋1，a＝9a₂a₆

(Ⅰ)若数列{b_n}满足：b_n＝＋lna_n，求数列{b_n}的前n项和S_n；

(Ⅱ)设c_n＝log₃a₁＋log₃a₂＋…＋log₃a_n，T_n＝＋＋…＋，求使≥(7－2n)T_n恒成立的实数的取值范围．

某中学经市人民政府批准建分校，工程从2010年底开工到2013年底完工，工程分三期完成．经过初步招投标淘汰后，确定只由甲、乙两家建筑公司承建，且每期工程由两公司之一独立承建，必须在建完前一期工程后再建后一期工程．己知甲公司获得第一期、第二期、第三期工程承包权的概率分别为、、．

(1)求甲、乙两公司各至少获得一期工程的概率；

(2)求甲公司获得工程期数ξ的分布列和数学期望Eξ．

如图所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，BC∥EF，BC＝2AD＝4，EF＝3，AE＝BE＝2，G是BC的中点．

(1)求证：BD⊥EG；

(2)求平面DEG与平面DEF所成二面角的大小．

已知向量＝(sinx，1＋cos2x)，＝(sinx－cosx，cos2x＋)，定义函数f(x)＝·(－)

(Ⅰ)求函数f(x)的单调递增区间；

(Ⅱ)在△ABC中，∠A为锐角且A＋B＝，f(A)＝－1，求边AC的长．

已知函数f(x)＝，数列{a_n}满足：a_n＞0，a₁＝1，a_n＋1＝f(a_n)，n∈N^*．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若b_n＝＋1，对任意正整数n，不等式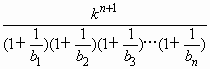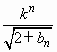－≤0恒成立，求正数k的取值范围．

已知函数．f(x)＝ax³－x²＋cx＋d(a，c，d∈R，a≠0)满足f(0)＝0，(1)＝0，且f(x)在R上单调递增．

(1)求f(x)的解析式；

(2)若g(x)＝(x)－mx在区间[m，m＋2]上的最小值为－5，求实数m的值．

已知数列他{b_n}满足b_n＋1＝b_n＋，且b₁＝，T_n为{b_n}的前n项和．

(1)求证：数列{b_n－}是等比数列，并求{b_n}的通项公式；

(2)如果对于任意n∈N_＋，不等式≥2n－7恒成立，求实数K的取值范围．

某中学经市人民政府批准建分校，工程从2010年底开工到2013年底完工，工程分三期完成．经过初步招投标淘汰后，确定只由甲、乙两家建筑公司承建，且每期工程由两公司之一独立承建，必须在建完前一期工程后再建后一期工程．已知甲公司获得第一期、第二期、第三期

工程承包权的概率分别为、、．

(1)求甲、乙两公司爷军伞获得一期工程的概率；

(2)求甲公司获得工程期数不超过两次的概率．