如图，五面体ABCDE中，正△ABC的边长为1，AE⊥平面ABC，CD∥AE，且CD＝AE．

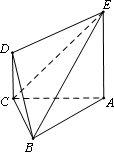
(Ⅰ)设CE与平面ABE所成的角为α，AE＝k(k＞0)，若α∈[，]，求k的取值范围；

(Ⅱ)在(I)和条件下，当k取得最大值时，求平面BDE与平面ABC所成角的大小．

某地区试行高考考试改革：在高三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试．假设某学生每次通过测试的概率都是1/3，每次测试通过与否互相独立．规定：若前4次都没有通过测试，则第5次不能参加测试

(1)求该学生考上大学的概率．

(2)记该生参加测试的次数为ξ，求ξ的分布列及ξ的数学期望．

在△ABC中，A，B，C的对边分别为a，b，c，且acosC，bcosB，ccosA成等差数列．

(Ⅰ)求B的值；

(Ⅱ)求2sin²A＋cos(A－C)的范围．

已知数列{a_n}中，a₁＝1，a₂＝，且a_n+1＝．(n＝2，3，4，…)．

(1)求a₃、a₄的值；

(2)设b_n＝－1(n∈N^*)，试用b_n表示b_n+1并求{a_n}的通项公式

(3)求证：对一切n∈N^*且n≥2，有a＋a＋…＋a＜．

已知函数f(x)＝x³＋3ax－1，g(x)＝(x)－ax－5，其中(x)是f(x)导函数

(Ⅰ)对满足－1≤a≤1的一切a的值，都有g(x)＜0，求实数的取值范围；

(Ⅱ)设a＝－m²，当实数m在什么范围内变化时，函数y＝f(x)的图象与直线y＝3只有一个公共点．

设数列{a_n}满足a₁＋2a₂＋3a₃＋…＋na_n＝2ⁿ(n∈N^*)．

(Ⅰ)求数列{a_n}的通项；

(Ⅱ)设b_n＝n²a_n，求数列{b_n}的前n项和S_n．

如图，五面体ABCDE中，正△ABC的边长为1，AE⊥平面ABC，CD∥AE，且CD＝AE．

(Ⅰ)设CE与平面ABE所成的角为α，AE＝k(k＞0)，若α＝[，]，求k的取值范围；

(Ⅱ)在(Ⅰ)和条件下，当k取得最大值时，求平面BDE与平面ABC所成角的大小．

某校2012年推优班报名正在进行，甲、乙、丙、丁四名学生跃跃欲试，现有四门学科(数学、物理、化学、信息技术)可供选择，每位学生只能任选其中一科．

(1)求恰有两门学科被选择的概率；

(2)已知报名后，丁已指定被录取．另外甲被录取的概率为，乙被录取的概率为，丙被录取的概率为．求甲、乙、丙三人中至少有两人被录取的概率．

在△ABC中，A，B，C的对边分别为a，b，c，且acosC，bcosB，ccosA成等差数列

(Ⅰ)求B的值；

(Ⅱ)求2sin²A＋cos(A－C)的范围．

(理科)已知{a_n}是递增数列，其前n项和为S_n，a₁＞1，且10S_n＝(2a_n＋1)(a_n＋2)，n∈N^*．

(Ⅰ)求数列{a_n}的通项a_n；

(Ⅱ)是否存在m，n，k∈N^*，使得2(a_m＋a_n)＝a_k成立？若存在，写出一组符合条件的m，n，k的值；若不存在，请说明理由；

(Ⅲ)设，，若对于任意的n∈N^*，不等式恒成立，求正整数m的最大值．