已知数列{a_n}中，a₁＝1，a₂＝3，且a_n+1＝a_n＋2a_n－1(n≥2)．

(1)设b_n＝a_n+1＋λa_n，是否存在实数λ，使数列{b_n}为等比数列．若存在，求出λ的值，若不存在，请说明理由；

(2)求数列{a_n}的前n项和S_n．

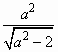设椭圆M：＝1(a＞)的右焦点为F₁，直线l：x＝与x轴交于点A，若(其中O为坐标原点)．

(1)求椭圆M的方程；

(2)设P是椭圆M上的任意一点，EF为圆N：x²＋(y－2)²＝1的任意一条直径(E、F为直径的两个端点)，求·的最大值．

已知正方形ABCD的边长为2，AC∩BD＝O．将正方形ABCD沿对角线BD折起，使AC＝a，得到三棱锥A－BCD，如图所示．

(1)当a＝2时，求证：AO⊥平面BCD；

(2)当二面角A－BD－C的大小为120°时，求二面角A－BC－D的正切值．

某城市为准备参加“全国文明城市”的评选，举办了“文明社区”评选的活动，在第一轮暗访评分中，评委会对全市50个社区分别从“居民素质”和“社区服务”两项进行评分，每项评分均采用5分制，若设“社区服务”得分为x分，“居民素质”得分为y分，统计结果如下表：

(1)若“居民素质”得分和“社区服务”得分均不低于3分(即x≥3且y≥3)的社区可以进入第二轮评比，现从50个社区中随机选取一个社区，求这个社区能进入第二轮评比的概率；

(2)若在50个社区中随机选取一个社区，这个社区的“居民素质”得分y的均值(即数学期望)为，求a、b的值．

如图，在△ABC中，点D在BC边上，AD＝33，sin∠BAD＝，cos∠ADC＝．

(1)求sin∠ABD的值；

(2)求BD的长．

已知函数f(x)＝－x³＋x²－2x(a∈R)．

(1)当a＝3时，求函数f(x)的单调区间；

(2)若对于任意x∈[1，＋∞)都有(x)＜2(a－1)成立，求实数a的取值范围；

(3)若过点(0，－)可作函数y＝f(x)图象的三条不同切线，求实数a的取值范围．

设椭圆M：(a＞)的右焦点为F₁，直线l：x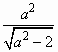＝与x轴交于点A，若0(其中O为坐标原点)．

(1)求椭圆M的方程；

(2)设P是椭圆M上的任意一点，EF为圆N：x²＋(y－2)²＝1的任意一条直径(E、F为直径的两个端点)，求·的最大值．

如图所示，已知正方形ABCD的边长为2，AC∩BD＝O．将正方形ABCD沿对角线BD折起，得到三棱锥A－BCD．

(1)求证：平面AOC⊥平面BCD；

(2)若三棱锥A－BCD的体积为，求AC的长．

各项均为正数的数列{a_n}，满足a₁＝1，a－＝2(n∈N^*)．

(1)求数列{a_n}的通项公式；

(2)求数列{}的前n项和S_n．

某城市为准备参加“全国文明城市”的评选，举办了“文明社区”评选的活动，在第一轮暗访评分中，评委会对全市50个社区分别从“居民素质”和“社区服务”两项进行评分，每项评分均采用5分制，若设“社区服务”得分为x分，“居民素质”得分为y分，统计结果如下表：

(1)若“居民素质”得分和“社区服务”得分均不低于3分(即x≥3且y≥3)的社区可以进入第二轮评比，现从50个社区中随机选取一个社区，求这个社区能进入第二轮评比的概率；

(2)若在50个社区中随机选取一个社区，这个社区的“居民素质”得1分的概率为，求a、b的值．