因发生意外交通事故，一辆货车上的某种液体泄露到一鱼塘中．为治理污染，根据环保部门的建议，现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂．已知每投放a(1≤a≤4，且a∈R)个单位的药剂，它在水中释放的浓度y(克/升)随着时间(天)变化的函数关系式近似为y＝a·f(x)，其中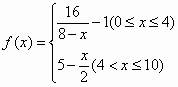．若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4(克/升)时，它才能起到有效的治污的作用．

(Ⅰ)若一次投放4个单位的药剂，则有效治污的时间可达几天？

(Ⅱ)若因材料紧张，第一次只能投放2个单位的药剂，6天后再投放a个单位的药剂，要使接下来的4天中能够持续有效治污，试求a的最小值(精确到0.1，参考数据：取1.4)．

已知以原点O为中心的椭圆，它的短轴长为，右焦点F(c，0)(c＞0)，它的长轴长为2a(a＞c＞0)，直线与x轴相交于点A，|OF|＝2|FA|，过点A的直线与椭圆相交于P、Q两点．

(Ⅰ)求椭圆的方程和离心率；

(Ⅱ)若·＝0，求直线PQ的方程；

因发生意外交通事故，一辆货车上的某种液体泄露到一鱼塘中．为治理污染，根据环保部门的建议，现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂．已知每投放a(1≤a≤4，且a∈R)个单位的药剂，它在水中释放的浓度y(克/升)随着时间(天)变化的函数关系式近似为y＝a·f(x)，其中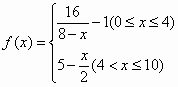．若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4(克/升)时，它才能起到有效的治污的作用．

(Ⅰ)若一次投放4个单位的药剂，则有效治污的时间可达几天？

(Ⅱ)若因材料紧张，第一次只能投放2个单位的药剂，6天后再投放a个单位的药剂，要使接下来的4天中能够持续有效治污，试求a的最小值(精确到0.1，参考数据：取1.4)．

对于项数为m的有穷数列{a_n}，记b_k＝max{a₁，a₂，…，a_k}(k＝1，2，…，m)，即b_k为a₁，a₂，…，a_k中的最大值，并称数列{b_n}是{a_n}的控制数列，如1，3，2，5，5的控制数列是1，3，3，5，5．

(1)若各项均为正整数的数列{a_n}的控制数列为2，3，4，5，5，写出所有的{a_n}；

(2)设{b_n}是{a_n}的控制数列，满足a_k＝b_m－k+1＝C(C为常数，k＝1，2，…，m)，求证：b_k＝a_k(k＝1，2，…，m)；

(3)设m＝100，常数a∈(，1)，若a_n＝an²－(－1)n，{b_n}是{a_n}的控制数列，求(b₁－a₁)＋(b₂－a₂)＋…＋(b₁₀₀－a₁₀₀)．

在平面直角坐标系xOy中，已知双曲线C：2x²－y²＝1．

(1)设F是C的左焦点，M是C右支上一点，若|MF|＝2，求点M的坐标；

(2)过C的左焦点作C的两条渐近线的平行线，求这两组平行线围成的平行四边形的面积；

(3)设斜率为k(|k|＜)的直线l交C于P、Q两点，若l与圆x²＋y²＝1相切，求证：OP⊥OQ．

海事救援船对一艘失事船进行定位：以失事船的当前位置为原点，以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度)，则救援船恰好在失事船正南方向12海里A处，如图，现假设：①失事船的移动路径可视为抛物线y＝；②定位后救援船即刻沿直线匀速前往救援；③救援船出发t小时后，失事船所在位置的横坐标为7t．

(1)当t＝0.5时，写出失事船所在位置P的纵坐标，若此时两船恰好会合，求救援船速度的大小和方向；

(2)问救援船的时速至少是多少海里才能追上失事船？

已知f(x)＝lg(x＋1)．

(1)若0＜f(1－2x)－f(x)＜1，求x的取值范围；

(2)若g(x)是以2为周期的偶函数，且当0≤x≤1时，g(x)＝f(x)，求函数y＝g(x)(x∈[1，2])的反函数．

如图，在三棱锥P－ABC中，PA⊥底面ABC，D是PC的中点，已知∠BAC＝，AB＝2，AC＝2，PA＝2，求：

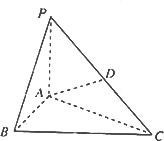
(1)三棱锥P－ABC的体积；

(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示)．

设函数f(x)＝＋sinx的所有正的极小值点从小到大排成的数列为{x_n}．

(Ⅰ)求数列{x_n}的通项公式；

(Ⅱ)设{x_n}的前n项和为S_n，求sinS_n．

如图，F₁，F₂分别是椭圆C：＋＝1(a＞b＞0)的左、右焦点，A是椭圆C的顶点，B是直线AF₂与椭圆C的另一个交点，∠F₁AF₂＝60°．

(Ⅰ)求椭圆C的离心率；

(Ⅱ)已知△AF₁B的面积为40，求a，b的值．