已知函数f(x)＝| x－1| ，g(x)＝－| x＋3| ＋a(a∈R)

(1)解关于x的不等式g(x)＞6；

(2)若函数y＝2f(x)的图像恒在函数y＝g(x)的图像的上方，求实数a的取值范围．

已知直线l的参数方程是(t是参数)圆C的极坐标方程为ρ＝2cos(＋)．

(1)求圆C在直角坐标系下的方程；

(2)由直线l上的点向圆引切线，求切线长的最小值．

A为圆外一点，AB，AC分别交圆于D，E，AB，AC的长分别是一元二次方程x²－x＋(m²－m＋)＝0的两个根．(如图所示)

(1)求m的值

(2)求证：DE∥BC

已知函数f(x)＝xlnx．

(1)求函数f(x)的单调区间和最小值；

(2)当b＞0时，求证：(其中e为自然对数的底数)；

(3)若a＞0，b＞0，求证：f(a)＋(a＋b)ln2≥f(a＋b)－f(b)．

如图所示，椭圆C：(a＞b＞0)的一个焦点为F(1，0)，且过点(2，0)．

(1)求椭圆C的方程；

(2)已知A、B为椭圆上的点，且直线AB垂直于x轴，又直线l：x＝4与x轴交于点N，直线AF与BN交于点M．

(ⅰ)求证：点M恒在椭圆C上；

(ⅱ)求△AMN面积的最大值．

如图示，四棱锥P－ABCD的底面是边长为1的正方形，PA^ CD，PA＝1，PD＝，E为PD上一点，PE＝2ED．

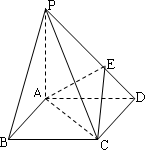
(1)求证：PA^ 平面ABCD；

(2)求二面角D－AC－E的正切值；

(3)在侧棱PC上是否存在一点F，使得BF∥平面AEC？若存在，指出F点的位置，并证明；若不存在，说明理由．

设不等式x²＋y²≤4确定的平面区域为U，ï xï ＋ï yï ≤1确定的平面区域为V．

(1)定义横、纵坐标为整数的点为“整点”，在区域U内任取3个整点，求这些整点中恰有2个整点在区域V的概率；

(2)在区域U内任取3个点，记这3个点在区域V的个数为X，求X的分布列和数学期望EX．

若数列{ a_n} 是等比数列，a₁＞0，公比q≠1，已知lna₁和2＋lna₅的等差中项为lna₂，且a₁a₂＝e．

(1)求{ a_n} 的通项公式；

(2)设b_n＝(n∈N* )，求数列{ b_n} 的前n项和．

关于x的不等式lg(|x＋3|－|x－7|)＜m．

(Ⅰ)当m＝1时，解此不等式；

(Ⅱ)设函数f(x)＝lg(|x＋3|－|x－7|)，当m为何值时，f(x)＜m恒成立？

已知在平面直角坐标系xOy内，点P(x，y)在曲线C：(为参数∈R)上运动．以Ox为极轴建立极坐标系，直线l的极坐标方程为ρcos(＋)＝0．

(Ⅰ)写出曲线C的标准方程和直线l的直角坐标方程；

(Ⅱ)若直线l与曲线C相交于A、B两点，点M在曲线C上移动，试求△ABM面积的最大值．