设等差数列{a_n}的前n项和为S_n，已知a₅＝－3，S₁₀＝－40

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若数列{a_bn}为等比数列，且b₁＝5，b₂＝8，令，若对任意的n∈N^*，有c_n≥c_k成立，求正整数k的值．

在△ABC中，角A，B，C的对边分别是a，b，c．已知a＝2c，且A－C＝．

(Ⅰ)求cosC的值；

(Ⅱ)当b＝1时，求△ABC的面积S的值．

已知椭圆C₁：＋＝1(a＞b＞0)和椭圆C₂：x²＋y²＝r²都过点(0，－1)，且椭圆C₁的离心率为．

(Ⅰ)求椭圆C₁和C₂的方程；

(Ⅱ)如图，A，B分别为椭圆C₁的左右顶点，P(x₀，y₀)为圆C₂上的动点．过点P作圆C₂的切线l，交椭圆C₁与不同的两点C，D，且l与x轴的交点为M，直线AC与直线DB的交点为N．

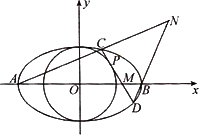
(i)求切线l的方程；

(ii)问点M，N的横坐标之积是否为定值？若是定值，求出此定值；若不是定值，请说明理由．

已知函数f(x)＝lnx－＋(a－1)x－，其中a＞－1且a≠0．

(Ⅰ)当a＞0时，求函数f(x)的单调区间；

(Ⅱ)若函数f(x)有两个相异的零点x₁，x₂，求实数a的取值范围．

在如图1所示的四边形ABCD中，∠ABD＝∠BDC＝，∠C＝，AB＝BD＝2．现将△ABD沿BD翻折，如图2所示．

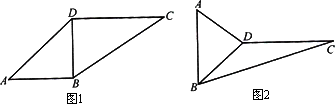
(Ⅰ)若二面角A－BD－C为直二面角，求证：AB⊥DC；

(Ⅱ)设E为线段BC上的点，当△ABE为等边三角形时，求二面角A－BD－C的余弦值．

设等差数列{a_n}的前n项和为S_n，已知a₅＝－3，S₁₀＝－40

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若数列{a_bn}为等比数列，且b₁＝5，b₂＝8，求数列{b_n}的前n项和T_n．

在△ABC中，角A，B，C的对边分别是a，b，c．已知a＝2c，且A－C＝．

(Ⅰ)求cosC的值；

(Ⅱ)当b＝1时，求△ABC的面积S的值．

已知函数f(x)＝(ax²＋bx＋c)e^－x(a≠0)的图像过点(0，－2)，且在该点的切线方程为4x－y－2＝0．

(Ⅰ)若f(x)在[2，＋∞)上为单调增函数，求实数a的取值范围；

(Ⅱ)若函数F(x)＝f(x)－m恰好有一个零点，求实数m的取值范围．

如图，过点D(0，－2)作抛物线x²＝2py(p＞0)的切线l，切点A在第二象限．

(Ⅰ)求切点A的纵坐标；

(Ⅱ)若离心率为的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k₁，k₂，若k₁＋2k₂＝4k，求椭圆方程．

如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA＝PD＝2，BC＝AD＝1，CD＝．

(Ⅰ)求证：平面PQB⊥平面PAD；

(Ⅱ)设PM＝tMC，若二面角M－BQ－C的平面角的大小为30°，试确定t的值．