某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2))．已知图(1)中身高在170～175 cm的男生人数有16人．

(Ⅰ)试问在抽取的学生中，男、女生各有多少人？

(Ⅱ)根据频率分布直方图，完成下列的2×2列联表，并判断能有多大(百分几)的把握认为“身高与性别有关”？

(Ⅲ)在上述80名学生中，从身高在170～175 cm之间的学生中按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率．

参考公式：K²＝

参考数据：

设△ABC的三个内角A，B，C所对的边分别为a，b，c．已知sin(A－)＝cosA．

(Ⅰ)求角Ａ的大小；

(Ⅱ)若a＝2，求b＋c的最大值．

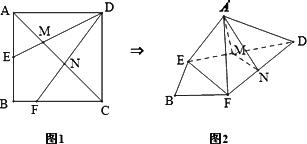
如图1，在正方形ABCD中，AB＝2，E是AB边的中点，F是BC边上的一点，对角线AC分别交DE、DF于M、N两点．将△DAE，△DCF折起，使A、C重合于点，构成如图2所示的几何体．

(Ⅰ)求证：D⊥面EF；

(Ⅱ)试探究：在图1中，F在什么位置时，能使折起后的几何体中EF∥平面AMN，并给出证明．

等比数列{a_n}的各项均为正数，且a₂＝2，a₄＝．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设b_n＝log₂a_n，求数列b_n的前n项和T_n．

顶点在坐标原点，开口向上的抛物线经过点A₀(1，1)，过点A₀作抛物线的切线交x轴于点B₁，过点B₁作x轴的垂线交抛物线于点A₁，过点A₁作抛物线的切线交x轴于点B₂，…，过点A_n(x_n，y_n)作抛物线的切线交x轴于点B_n+1(x_n+1，0)．

(Ⅰ)求数列{x_n}，{y_n}的通项公式(n∈N^*)；

(Ⅱ)设，数列{a_n}的前n项和为T_n．求证：；

(Ⅲ)设b_n＝1－log₂y_n，若对于任意正整数n，不等式…≥成立，求正数a的取值范围．

已知函数f(x)＝alnx－ax－3(a∈R)．

(Ⅰ)当a＝1时，求函数f(x)的单调区间；

(Ⅱ)若函数y＝f(x)的图象在点(2，f(2))处的切线的倾斜角为45°，问：m在什么范围取值时，对于任意的t∈[1，2]，函数g(x)＝x³＋x²[＋(x)]在区间(t，3)上总存在极值？

如图：⊙O方程为x²＋y²＝4，点P在圆上，点D在x轴上，点M在DP延长线上，⊙O交y轴于点N，∥．且＝．

(Ⅰ)求点M的轨迹C的方程；

(Ⅱ)设，若过F₁的直线交(I)中曲线C于A、B两点，求的取值范围．

一个四棱椎的三视图如图所示：

(Ⅰ)求证：PA⊥BD；

(Ⅱ)在线段PD上是否存在一点Q，使二面角Q－AC－D的平面角为30°？若存在，求的值；若不存在，说明理由．

形状如图所示的三个游戏盘中(图(1)是正方形，M、N分别是所在边中点，图(2)是半径分别为2和4的两个同心圆，O为圆心，图(3)是正六边形，点P为其中心)各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．

(Ⅰ)一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？

(Ⅱ)用随机变量ξ表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量ξ的分布列及数学期望．

已知函数f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，|φ|＜，x∈R)的图象的一部分如下图所示．

(Ⅰ)求函数f(x)的解析式；

(Ⅱ)求函数y＝f(x)＋f(x＋2)的最大值与最小值．