某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的以O为圆心的转盘一次，并获得相应金额的返券，假定指针等可能地指向任一位置(不指向各区域的边界)．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

(Ⅰ)若某位顾客消费128元，求返券金额不低于30元的概率；

(Ⅱ)若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X(元)．求随机变量X的分布列和数学期望．

如图，四棱锥P－ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC＝4，O为BD的中点，E为PA的中点．

(Ⅰ)求证：PO·⊥平面ABCD；

(Ⅱ)求证：OE∥平面PDC；

(Ⅲ)求直线CB与平面PDC所成角的正弦值．

已知函数f(x)＝Msin(ωx＋)(M＞0，||＜)的部分图象如图所示．

(Ⅰ)求函数f(x)的解析式；

(Ⅱ)在△ABC中，角A、B、C的对边分别是a、b、c，若(2a－c)cosB＝bcosC，求f()的取值范围．

设函数f(x)＝－x³＋ax²＋a²x＋1(x∈R)，其中a∈R．

(Ⅰ)当a＝1时，求曲线y＝f(x)在点(2，f(2))处的切线方程；

(Ⅱ)当a＞0时，求函数f(x)的极大值和极小值；

(Ⅲ)当a＝2时，是否存在函数y＝f(x)图像上两点以及函数y＝(x)图像上两点，使得以这四点为顶点的四边形ABCD同时满足如下三个条件：①四边形ABCD是平行四边形：②AB⊥x轴；③|AB|＝4．

若存在，指出四边形ABCD的个数；若不存在，说明理由．

已知点A(－1，O)，B(1，0)，动点M的轨迹曲线C满足∠AMB＝2，||·||cos²＝3

(Ⅰ)求曲线C的方程；

(Ⅱ)试探究曲线C上是否存在点P，使直线PA与PB的斜率k_PA·k_PB＝1？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标)．

已知数列{a_n}的前n项为和S_n，点(n，)在直线y＝x＋上．数列{b_n}满足b_n+2－2b_n+1＋b_n＝0(n∈N^*)，且b₃＝11，前9项和为153．

(Ⅰ)求数列{a_n}、{b_n}的通项公式；

(Ⅱ)设f(n)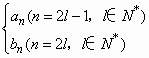＝，问是否存在m∈N^*，使得f(m＋15)＝5f(m)成立？若存在，求出m的值；若不存在，请说明理由．

如图，正三棱锥O－ABC的三条侧棱OA，OB，OC两条垂直，且长度为2．E，F分别是AB，AC的中点，H是EF的中点，过EF的一个平面与侧棱OA，OB，OC或其延长线分别相交于A₁，B₁，C₁，已知OA₁＝．

(Ⅰ)证明：B₁C₁⊥平面OAH；

(Ⅱ)求三棱锥O－A₁B₁C₁体积．

如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动)，且箭头A指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘，得分记为(a，b)(假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动)．

(Ⅰ)请列出一个家庭得分(a，b)的所有情况；

(Ⅱ)若游戏规定：一个家庭的总得分为参与游戏的两人所得分数之和，且总得分为偶数的家庭可以获得一份奖品．请问一个家庭获奖的概率为多少？

如图，在平面直角坐标系中，锐角α和钝角β 的终边分别与单位圆交于A，B两点．

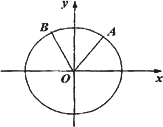
(Ⅰ)如果A、B两点的纵坐标分别为、、求COSα和sinβ：

(Ⅱ)在(Ⅰ)的条件下，求cos(β－α)的值：

(Ⅲ)已知点C(－1，)，求函数f(a)＝·的值域

已知a为实数，数列{a_n}满足a₁＝a，当n≥2时，a_n＝

(1)当a＝100时，求数列{a_n}的前100项的和S₁₀₀；

(2)证明：对于数列{a_n}，一定存在k∈N^*，使0＜a_k≤3；

(3)令b_n＝，当2＜a＜3时，求证：．