如图，四边形DCBE为直角梯形，∠DCB＝90°，DE∥CB，DE＝1，BC＝2，又AC＝1，∠ACB＝120°，CD⊥AB，直线AE与直线CD所成角为60°．

(Ⅰ)求证：平面ACD⊥平面ABC；

(Ⅱ)求BE与平面ACE所成角的正弦值．

如图，AB是底部B不可到达的一个塔型建筑物，A为塔的最高点．现需在对岸测出塔高AB，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底B在同一水平面内的一条基线CD，使C，D，B三点不在同一条直线上，测出∠DCB及∠CDB的大小(分别用α，β表示测得的数据)以及C，D间的距离(用 s表示测得的数据)，另外需在点C测得塔顶A的仰角(用表示测量的数据)，就可以求得塔高AB．乙同学的方法是：选一条水平基线EF，使E，F，B三点在同一条直线上．在E，F处分别测得塔顶A的仰角(分别用α，β表示测得的数据)以及E，F间的距离(用 s表示测得的数据)，就可以求得塔高AB．

请从甲或乙的想法中选出一种测量方法，写出你的选择并按如下要求完成测量计算：

①画出测量示意图；

②用所叙述的相应字母表示测量数据，画图时C，D，B按顺时针方向标注，E，F按从左到右的方向标注；

③求塔高AB．

已知△ABC的三边长|AB|＝，|BC|＝4，|AC|＝1动点M满足＝λ＋μ，且λμ＝，

(1)求||最小值，并指出此时与，的夹角；

(2)是否存在两定点F₁，F₂使|||－|||恒为常数K？若存在，指出常数K的值，若不存在，说明理由

已知数列{a_n}满足a₁＝1，a₂＝5，n≥2时，a_n+1＝5a_n－6a_n－1．

(1)证明：数列{a_n+1－3a_n}为等比数列，并求数列{a_n}的通项公式a_n；

(2)试比较a_n与2n²＋1的大小，并说明理由．

在四梭锥P－ABCD中，底面ABCD是边长为1的正方形，且PA⊥面ABCD．

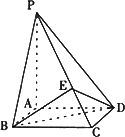
(1)求证：PC⊥BD；

(2)过直线BD且垂直于直线PC的平面交PC于点E，且三梭锥E－BCD的体积取到最大值，

(1)求此时四棱锥E－ABCD的高；

(2)求二面角A－DE－B的余弦值的大小．

食品安全已引起社会的高度关注，卫生监督部门加大了对食品质量检测，已知某种食品的合格率为0.9、现有8盒该种食品，质检部门对其逐一检测

(1)求8盒中恰有4盒合格的概率(保留三位有效数字)

(2)设检测合格的盒数为随机变量ξ求ξ的数学期望Eξ．

将函数y＝sinωxcos－cosωxsin(ω＞0，0＜＜π)的图像上各点的横坐标伸长为原来的2倍(纵坐标不变)，再向左平移个单位，得到函数y＝f(x)的图像，若函数y＝f(x)的图像过点(，0)，且相邻两对称轴间的距离为．

(1)求ω，的值；

(2)若锐角△ABC中A、B、C成等差数列，且f(A)的取值范围．

已知函数f(x)＝|ax－2|＋blnx(x＞0)．

(1)若a＝1，f(x)在(0，＋∞)上是单调增函数，求b的取值范围；

(2)若a≥2，b＝1，求方程f(x)＝在(0，1]上解的个数．

已知数列{a_n}，a₁＝a，且a_n+1＋2a_n＝2ⁿ⁺¹(n∈N^*)，

(1)若a₁，a₂，a₃成等差数列，求实数a的值；

(2)数列{a_n}能为等比数列吗？若能，试写出它的充要条件并加以证明；若不能，请说明理由．

如图，已知椭圆C：＋y²＝1(a＞1)的上顶点为A，离心率为，若不过点A的动直线l与椭圆C相交于P、Q两点，且·＝0．

(Ⅰ)求椭圆C的方程；

(Ⅱ)求证：直线l过定点，并求出该定点N的坐标．