由数字1，2，3，4组成五位数，从中任取一个．

(1)求取出的数满足条件：“对任意的正整数j(1≤j≤5)，至少存在另一个正整数k(1≤k≤5)，且k≠j，使得a_j＝a_k”的概率；

(2)记ξ为组成该数的相同数字的个数的最大值，求ξ的概率分布列和数学期望．

选修4－2：矩阵与变换

已知矩阵A＝，矩阵B＝，直线l₁：x－y＋4＝0经矩阵A所对应的变换得到直线l₂，直线l₂又经矩阵B所对应的变换得到直线l₃：x＋y＋4＝0，求直线l₂的方程．

已知数列{a_n}单调递增，且各项非负，对于正整数K，若任意的i，j(1≤i≤j≤K)，a_j－a_i仍是{a_n}中的项，则称数列{a_n}为“K项可减数列”．

(1)已知数列{a_n}是首项为2，公比为2的等比数列，且数列{b_n－2}是“K项可减数列”，试确定K的最大值．

(2)求证：若数列{a_n}是“K项可减数列”，则其前n项的和．

(3)已知{a_n}是各项非负的递增数列，写出⑵的逆命题，判断该逆命题的真假，并说明理由．

已知函数f₁(x)＝e^|x－2a+1|，f₂(x)＝e^|x－a|+1，x∈R，1≤a≤6．

(1)若a＝2，求f(x)＝f₁(x)＋f₂(x)在[2，3]上的最小值；

(2)若|f₁(x)＝f₂(x)|＝f₂(x)－f₁(x)对于任意的实数x恒成立，求a的取值范围；

(3)求函数在[1，6]上的最小值．

已知椭圆的中心在原点， 焦点在x轴上，长轴长是短轴长的2倍，且经过点M(2，1)，平行于OM直线l在y轴上的截距为m(m＜0)，设直线l交椭圆于两个不同点A、B．

(1)求椭圆方程；

(2)求证：对任意的m的允许值，△ABM的内心I在定直线x＝2上．

据环保部门测定，某处的污染指数与附近污染源的强度成正比，与到污染源距离的平方成反比，比例常数为k(k＞0)．现已知相距18 km的A，B两家化工厂(污染源)的污染强度分别为a，b，它们连线上任意一点C处的污染指数y等于两化工厂对该处的污染指数之和．设AC＝x(km)．

(1)试将y表示为x的函数；

(2)若a＝1，且x＝6时，y取得最小值，试求b的值．

如图，在四棱锥A－BCDE中，底面BCDE是直角梯形，∠BED＝90°，BE∥CD，AB＝6，BC＝5，，侧面ABE⊥底面BCDE，∠BAE＝90°．

(1)求证：平面ADE⊥平面ABE；

(2)过点D作面α∥平面ABC，分别于BE，AE交于点F，G，求△DFG的面积．

已知函数f(x)＝|2x＋1|＋|2x－3|．

(Ⅰ)求不等式f(x)≤6的解集；

(Ⅱ)若关于x的不等式f(x)＞a恒成立，求实数a的取值范围．

已知函数f(x)＝lnx－x²＋x＋2．

(Ⅰ)求函数f(x)的单调区间；

(Ⅱ)若a＞0，求f(x)在区间(0，a]上的最大值；

(Ⅲ)设函数g(x)＝x³－(1＋2e)x²＋(m＋1)x＋2，(m∈R)，试讨论函数f(x)与g(x)图象交点的个数．

如图所示，在△DEM中，⊥，＝(0，－8)，N在y轴上，且＝(＋)，点E在x轴上移动．

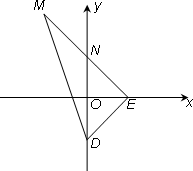
(Ⅰ)求点M的轨迹方程；

(Ⅱ)过点F(0，1)作互相垂直的两条直线l₁、l₂，l₁与点M的轨迹交于点A、B，l₂与点M的轨迹交于点C、D，求·的最小值．