已知AB为半圆O的直径，AB＝4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE＝1．

(Ⅰ)求证：AC平分∠BAD；

(Ⅱ)求BC的长．

如图，已知抛物线C：y²＝2px(p＞0)和⊙M：(x－4)²＋y²＝1，过抛物线C上一点H(x₀，y₀)(y₀≥1)作两条直线与⊙M相切于A、B两点，分别交抛物线于E，F两点，圆心点M到抛物线准线的距离为．

(Ⅰ)求抛物线C的方程；

(Ⅱ)当∠AHB的角平分线垂直x轴时，求直线EF的斜率；

(Ⅲ)若直线AB在y轴上的截距为t，求t的最小值．

已知函数f(x)＝ax－1－lnx(a∈R)．

(Ⅰ)讨论函数f(x)在定义域内的极值点的个数；

(Ⅱ)已知函数f(x)在x＝1处取得极值，且对x∈(0，＋∞)，f(x)≥bx－2恒成立，求实数b的取值范围．

如图，在四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD为长方形，AD＝2AB，点E、F分别是线段PD、PC的中点．

(Ⅰ)证明：EF∥平面PAB；

(Ⅱ)在线段AD上是否存在一点O，使得BO⊥平面PAC，若存在，请指出点O的位置，并证明BO⊥平面PAC；若不存在，请说明理由．

已知向量m＝(sin2＋，sinx)，n＝(cos2x－sin2x，2sinx)，函数f(x)＝m·n．

(Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)若，求函数f(x)值域．

某种产品按质量标准分成五个等级，等级编号x依次为1，2，3，4，5．现从一批产品中随机抽取20件，对其等级编号进行统计分析，得到频率分布表如下：

(Ⅰ)若所抽取的20件产品中，等级编号为4的恰有3件，等级编号为5的恰有2件，求a，b，c的值；

(Ⅱ)在(I)的条件下，将等级编号为4的3件产品记为x₁，x₂，x₃，等级编号为5的2件产品记为y₁，y₂，现从x₁，x₂，x₃，y₁，y₂这5件产品中任取两件(假定每件产品被取出的可能性相同)，写出所有可能的结果，并求这两件产品的等级编号恰好相同的概率．

已知椭圆C：(a＞b＞0)．F₁，F₂分别为椭圆C的左，右焦点，A₁，A₂分别为椭圆C的左，右顶点．过右焦点F₂且垂直于x轴的直线与椭圆C在第一象限的交点为M(，2)．

(1)求椭圆C的标准方程；

(2)直线l：x＝my＋1与椭圆C交于P，Q两点，直线A₁P与A₂Q交于点S．当直线l变化时，点S是否恒在一条定直线上？若是，求此定直线方程；若不是，请说明理由．

已知函数f(x)＝(2－a)lnx＋＋2ax(a∈R)．

(1)当a＝0时，求f(x)的极值；

(2)当a＜0时，求f(x)单调区间；

(3)若对任意a∈(－3，－2)及x₁，x₂∈[1，3]，恒有(m＋ln3)a－ln3＞|f(x₁)－f(x₂)|成立，求实数m的取值范围．

设数列{a_n}满足条件：a₁＝8，a₂＝0，a₃＝－7，且数列{a_n+1－a_n}(n∈N^*)是等差数列．

(1)设c_n＝a_n+1－a_n，求数列{c_n}的通项公式；

(2)若b_n＝2ⁿ·c_n，求S_n＝b₁＋b₂＋…＋b_n；

(3)数列{a_n}的最小项是第几项？并求出该项的值．

在边长为a的正方形ABCD中，E，F分别为BC，CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥B－AEF，如图所示．

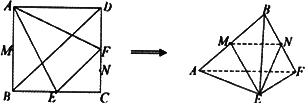
(1)在三棱锥B－AEF中，求证：AB⊥EF；

(2)求四棱锥E－AMNF的体积．