已知函数f(x)＝2sinx·cosx＋2cos²x＋m在区间[0，]上的最大值为2．

(Ⅰ)求常数m的值；

(Ⅱ)在△ABC中，角A，B，C所对的边是a，b，c，若f(A)＝1，sinB＝3sinC，△ABC面积为．求边长a．

(不等式选做题)若不等式|x＋1|＋|x－2|≥a对任意x∈R恒成立，则a的取值范围是________．

选修4－4：坐标系与参数方程

以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线l经过点P(1，1)，倾斜角α＝．

(1)写出直线l的参数方程；

(2)设l与圆ρ＝2相交于两点A、B，求点P到A、B两点的距离之积．

选修4－1几何证明选讲

如图，D，E分别是AB，AC边上的点，且不与顶点重合，已知AE＝m，AC＝n，AD，AB为方程x²－14x＋mn的两根

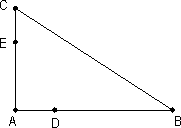
(1)证明C，B，D，E四点共圆；

(2)若∠A＝90°，m＝4，n＝6，求C，B，D，E四点所在圆的半径．

已知抛物线C：y²＝4x，F是C的焦点，过焦点F的直线l与C交于A，B两点，O为坐标原点．

(1)求·的值；(2)设＝λ，求△ABO的面积S的最小值；

(3)在(2)的条件下若S≤，求λ的取值范围．

已知函数(x)＝，a是正常数．

(1)若f(x)＝(x)＋lnx，且a＝，求函数f(x)的单调递增区间；

(2)若g(x)＝|lnx|＋(x)，且对任意的x₁，x₂∈(0，2〕，且x₁≠x₂，都有＜－1，求a的取值范围

在某次测验中，有6位同学的平均成绩为75分．用x_n表示编号为n(n＝1，2，…，6)的同学所得成绩，且前5位同学的成绩如下：

(1)求第6位同学成绩x₆，及这6位同学成绩的标准差s；

(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68，75)中的概率．

如图，四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB．

(1)求证：CE⊥平面PAD；

(2)若PA＝AB＝1，AD＝3，CD＝，∠CDA＝45°，求四棱锥P－ABCD的体积

在△ABC中，内角A，B，C的对边分别为a，b，c．已知．

(1)求的值；

(2)若cosB＝，△ABC的周长为5，求b的长．

在数列{a_n}和{b_n}中，a_n＝aⁿ，b_n＝(a＋1)n＋b，n＝1，2，3，…，其中a≥2且a∈N^*，b∈R．设A＝{a₁，a₂，a₃，…}，B＝{b₁，b₂，b₃，…}，试问在区间[1，a]上是否存在实数b使得C＝A∩B≠．若存在，求出b的一切可能的取值及相应的集合C；若不存在，试说明理由．