已知函数的最小正周期为π．

(Ⅰ)求的值；

(Ⅱ)讨论f(x)在区间[0，2]上的单调性．

已知椭圆的焦距为4，且过点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)设Q(x₀，y₀)(x₀y₀≠0)为椭圆C上一点，过点Q作x轴的垂线，垂足为E．取点A(0，2)，连接AE，过点A作AE的垂线交x轴于点D．点G是点D关于y轴的对称点，作直线QG，问这样作出的直线QG是否与椭圆C一定有唯一的公共点？并说明理由．

设函数f(x)＝ax－(1a²)x²，其中a＞0，区间I＝{x|f(x)＞0}．

(Ⅰ)求I的长度(注：区间(α，β)的长度定义为β－α；

(Ⅱ)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I长度的最小值．

如图，四棱锥P－ABCD的底面ABCD是边长为2的菱形，∠BAD＝60°．已知PB＝PD＝2，PA＝．

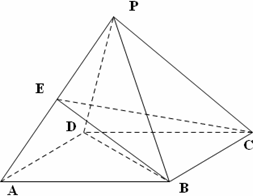
(Ⅰ)证明：PC⊥BD．

(Ⅱ)若E为PA的中点，求三菱锥P－BCE的体积．

为调查甲、乙两校高三年级学生某次联考数学成绩情况，用简单随机抽样，从这两校中各抽取30名高三年级学生，以他们的数学成绩(百分制)作为样本，样本数据的茎叶图如下：

(Ⅰ)若甲校高三年级每位学生被抽取的概率为0.05，求甲校高三年级学生总人数，并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格)；

(Ⅱ)设甲、乙两校高三年级学生这次联考数学平均成绩分别为，估计的值．

如图，点P(0，－1)是椭圆C₁： (a＞b＞0)的一个顶点，C₁的长轴是圆C₂：x²＋y²＝4的直径．l₁，l₂是过点P且互相垂直的两条直线，其中l₁交圆C₂于A，B两点，l₂交椭圆C₁于另一点D．

(Ⅰ)求椭圆C₁的方程；

(Ⅱ)求△ABD面积取最大值时直线l₁的方程．

如图，在四面体A－BCD中，AD^ 平面BCD，BC^ CD，AD＝2，BD＝2．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ＝3QC．

(Ⅰ)证明：PQ∥平面BCD；

(Ⅱ)若二面角C－BM－D的大小为60°，求Ð BDC的大小．

设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．

(Ⅰ)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；

(Ⅱ)从该袋子中任取(每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若Eη＝－，Dη＝，求a∶b∶c．

直线y＝kx＋m(m≠0)，W：相交于A，C两点，O是坐标原点

(1)当点B的坐标为(0，1)，且四边形OABC为菱形时，求AC的长．

(2)当点B在W上且不是W的顶点时，证明四边形OABC不可能为菱形．

已知函数f(x)＝x²＋xsinx＋cosx．

(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值．

(2)若曲线y＝f(x)与直线y＝b有两个不同的交点，求b的取值范围．