已知椭圆C：＋＝1(a＞b＞0)的左、右焦点分别为F₁，F₂，点M(0，2)是椭圆的一个顶点，△F₁MF₂是等腰直角三角形．

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k₁，k₂，且k₁＋k₂＝8，探究：直线AB是否过定点，并说明理由．

设函数f(x)＝(x²＋ax＋a)e^－x，其中x∈R，a是实常数，e是自然对数的底．

(1)确定a的值，使f(x)的极小值为0；

(2)讨论关于x的方程f(x)＋(x)＝2xe^－x＋x^－2(x≠0)的实数根的个数．

已知函数f(x)的图象在[a，b]上连续不断，定义：

，

其中，min{f(x)|x∈D}表示函数f(x)在区间上的最小值，max{f(x)|x∈D}表示函数f(x)在区间上的最大值．若存在最小正整数k，使得f₂(x)－f₁(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数为区间[a，b]上的“k阶收缩函数”．

(1)若f(x)＝cosx，x∈[0，π]，试写出f₁(x)，f₂(x)的表达式；

(2)已知函数f(x)＝x²，x∈[－1，4]，试判断f(x)是否为[－1，4]上的“k阶收缩函数”，如果是，求出相应的k；如果不是，请说明理由；

(3)已知b＞0函数f(x)＝－x³＋3x²是[0，b]上的2阶收缩函数，求b的取值范围．

已知函数

(1)若曲线y＝f(x)在点P(1，f(1))处的切线与直线y＝x＋2垂直，求函数y＝f(x)的单调区间；

(2)若对，都有恒成立，试求实数a的取值范围；

(3)记g(x)＝f(x)＋x－b，当a＝1时，函数g(x)在区间[e^－1，e]上有两个零点，求实数b的取值范围(e为自然对数的底数)．

(理)已知函数．

(Ⅰ)若函数有区间上存在极值(a＞0)，求实数a的取值范围；

(Ⅱ)如果当x≥1，不等式恒成立，求实数k的取值范围；

(Ⅲ)求证：[(n＋1)！]²＞(n＋1)·e^n－2(n∈N^*)．

已知a∈R，函数f(x)＝x³－3x²＋3ax－3a＋3

(Ⅰ)求曲线y＝f(x)在点(1，f(1))处的切线方程；

(Ⅱ)当x∈[0，2]时，求|f(x)|的最大值．

如图，已知椭圆C₁与C₂的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n(m＞n)，过原点且不与x轴重合的直线l与C₁，C₂的四个交点按纵坐标从大到小依次为A，B，C，D．记λ＝，△BDM和△ABN的面积分别为S₁和S₂．

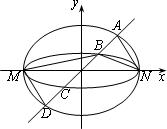
(Ⅰ)当直线l与y轴重合时，若S₁＝λS₂，求λ的值；

(Ⅱ)当λ变化时，是否存在与坐标轴不重合的直线l，使得S₁＝λS₂？并说明理由．

设a＞0，b＞0，已知函数f(x)＝．

(Ⅰ)当a≠b时，讨论函数f(x)的单调性；

(Ⅱ)当x＞0时，称f(x)为a、b关于x的加权平均数．

(ⅰ)判断f(1)，f()，f()是否成等比数列，并证明f()≤f()；

(ⅱ)a、b的几何平均数记为G．称为a、b的调和平均数，记为H．

若H≤f(x)≤G，求x的取值范围．