
科目: 来源: 题型:解答题
(本题满分12分)若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 接近
接近 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、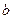 ,证明:
,证明: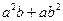 比
比 接近
接近 ;
;
(3)已知函数 的定义域
的定义域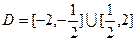 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
查看答案和解析>>
科目: 来源: 题型:解答题
(本题满分12分)
设函数 的定义域为
的定义域为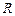 ,当
,当 时,
时,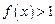 ,且对任意的实数
,且对任意的实数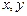 ,有
,有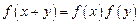 .
.
(Ⅰ)求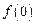 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;
(Ⅱ)数列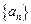 满足
满足 ,且
,且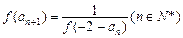
①求通项公式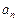 的表达式;
的表达式;
②令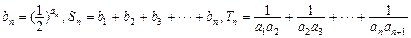 ,试比较
,试比较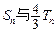 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目: 来源: 题型:解答题
为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度 与时间t满足关系式:
与时间t满足关系式: ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度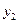 与时间t满足关系式:
与时间t满足关系式: 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com