
科目: 来源: 题型:解答题
每年的三月十二日,是中国的植树节,林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,规定高于128厘米的树苗为“良种树苗”,测得高度如下(单位:厘米):
甲:137,121,131,120,129,119,132,123,125,133;
乙:110,130,147,127,146,114,126,110,144,146.
(1)根据抽测结果,画出甲、乙两种树苗高度的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为x,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
(3)若小王在甲种树苗中随机领取了5株进行种植,用样本的频率分布估计总体分布,求小王领取到的“良种树苗”的株数X的分布列.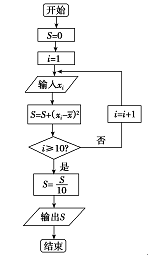
查看答案和解析>>
科目: 来源: 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 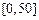 | 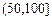 | 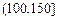 | 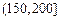 | 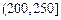 | 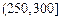 | 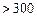 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
|
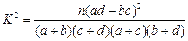
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目: 来源: 题型:解答题
一批产品需要进行质量检验,质检部门规定的检验方案是:先从这批产品中任取3件作检验,若3件产品都是合格品,则通过检验;若有2件产品是合格品,则再从这批产品中任取1件作检验,这1件产品是合格品才能通过检验;若少于2件合格品,则不能通过检验,也不再抽检. 假设这批产品的合格率为80%,且各件产品是否为合格品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费为125元,并且所抽取的产品都要检验,记这批产品的检验费为 元,求
元,求 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,一半径为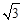 的圆形靶内有一个半径为
的圆形靶内有一个半径为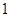 的同心圆,将大圆分成两
的同心圆,将大圆分成两
部分,小圆内部区域记为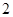 环,圆环区域记为
环,圆环区域记为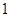 环,某同学向该靶投掷
环,某同学向该靶投掷 枚飞镖,每次
枚飞镖,每次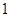 枚. 假设他每次必
枚. 假设他每次必
定会中靶,且投中靶内各点是随机的.
(1)求该同学在一次投掷中获得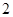 环的概率;
环的概率;
(2)设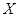 表示该同学在
表示该同学在 次投掷中获得的环数,求
次投掷中获得的环数,求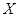 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为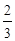 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为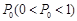 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为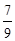 ,求
,求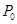 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目: 来源: 题型:解答题
某公司为招聘新员工设计了一个面试方案:应聘者从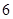 道备选题中一次性随机抽取
道备选题中一次性随机抽取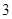 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中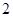 道题的便可通过.已知
道题的便可通过.已知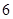 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成,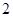 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是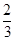 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
科目: 来源: 题型:解答题
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).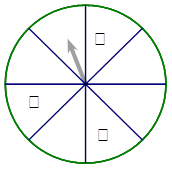
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为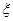 ,求
,求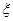 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
下图是预测到的某地5月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天
(1)求此人到达当日空气质量优良的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明).
查看答案和解析>>
科目: 来源: 题型:解答题
地为绿化环境,移栽了银杏树 棵,梧桐树
棵,梧桐树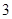 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别
为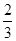 、
、 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的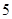 棵树中:
棵树中:
(1)求银杏树都成活且梧桐树成活 棵的概率;
棵的概率;
(2)求成活的棵树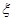 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目: 来源: 题型:解答题
第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京召开.为了做好两会期间的接待服务工作,中国人民大学学生实践活动中心从7名学生会干部(其中男生4人,女生3人)中选3人参加两会的志愿者服务活动.
(1)所选3人中女生人数为 ,求
,求 的分布列及数学期望:
的分布列及数学期望:
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com