
科目: 来源: 题型:解答题
甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为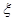 ;乙用这枚硬币掷2次,记正面朝上的次数为
;乙用这枚硬币掷2次,记正面朝上的次数为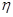 。
。
(1)分别求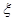 与
与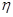 的期望;
的期望;
(2)规定:若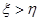 ,则甲获胜;若
,则甲获胜;若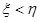 ,则乙获胜,分别求出甲和乙获胜的概率.
,则乙获胜,分别求出甲和乙获胜的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立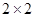 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
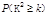 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
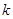 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
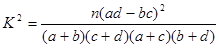 (
(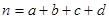 )
)查看答案和解析>>
科目: 来源: 题型:解答题
数学试题中有12道单项选择题,每题有4个选项。某人对每道题都随机选其
中一个答案(每个选项被选出的可能性相同),求答对多少题的概率最大?并求出此种情况下概
率的大小.(可保留运算式子)
查看答案和解析>>
科目: 来源: 题型:解答题
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为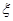 ,求
,求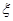 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
甲,乙两人进行射击比赛,每人射击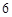 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
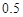 的概率.
的概率.查看答案和解析>>
科目: 来源: 题型:解答题
对关于 的一元二次方程
的一元二次方程 ……
…… ,解决下列两个问题:
,解决下列两个问题:
(1)若 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,求方程
三个数中任取的一个数,求方程 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求方程
任取的一个数,求方程 有两个不相等实根的概率.
有两个不相等实根的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| | 员工号 | 1 | 2 | 3 | 4 |
| 甲组 | 件数 | 9 | 11 | 1l | 9 |
| | 员工号 | 1 | 2 | 3 | 4 |
| 乙组 | 件数 | 9 | 8 | 10 | 9 |
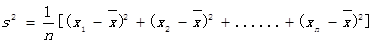 ,其中
,其中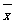 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)查看答案和解析>>
科目: 来源: 题型:解答题
某学校篮球队、羽毛球队、乒乓球队的某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是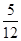 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是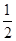 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?
查看答案和解析>>
科目: 来源: 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com