
科目: 来源:不详 题型:单选题
| A.5 | B.11 | C.29 | D.43 |
查看答案和解析>>
科目: 来源:重庆市期末题 题型:解答题
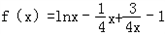 .
.查看答案和解析>>
科目: 来源:期末题 题型:解答题
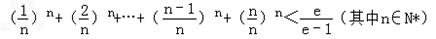 .
.查看答案和解析>>
科目: 来源:湖南省月考题 题型:解答题
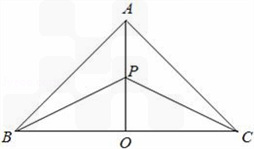
查看答案和解析>>
科目: 来源:北京市月考题 题型:解答题
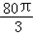 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.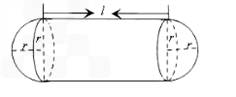
查看答案和解析>>
科目: 来源:东至县一模 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com