
科目: 来源: 题型:
已知数列{an}中,a1=1,an+1= (an+
(an+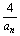 )(n∈N*),且{an}存在极限。
)(n∈N*),且{an}存在极限。
(1)证明:{an}时先增后减数列,并求an的最大值;
(2)已知圆锥曲线Cn的方程为: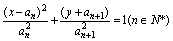 设
设 Cn=C,求曲线C的方程并求曲线C的面积。
Cn=C,求曲线C的方程并求曲线C的面积。
查看答案和解析>>
科目: 来源: 题型:
已知点集L={(x,y)|y=m·n},其中m=(2x-b,1),n=(1,b+1),点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,n∈N+.
(1)求数列{an},{bn}的通项公式;
(2)若Cn= 求
求 (c1+c2+…+cn);
(c1+c2+…+cn);
查看答案和解析>>
科目: 来源: 题型:
某学生在体育训练时弄伤了膝关节,医生给开了一些消炎药,并嘱咐每天早晚8点各服用一片药片,已知该药品 每征220m
每征220m g,他的贤脏每次12小时从体内滤出这种药的60%,如果这种药在体内残留超过386mg,将产生副作用。
g,他的贤脏每次12小时从体内滤出这种药的60%,如果这种药在体内残留超过386mg,将产生副作用。
请问:(1)该同学上午8时第一次服药后,到第二天早晨服药后,药在体内还残留多少?
(2)该同学若长期服用该药,会不会产生副作用?
查看答案和解析>>
科目: 来源: 题型:
若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意正整数an=-2(n+1),Tn-3S=4n.
(Ⅰ)求数列{bn}的通项公式;
( Ⅱ)在平面直角坐标系内,直线ln的斜率为bn.且与曲线y=x2有且仅一个交点,与y轴交于Dn,记dn=
Ⅱ)在平面直角坐标系内,直线ln的斜率为bn.且与曲线y=x2有且仅一个交点,与y轴交于Dn,记dn=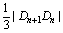 -(2n+7)求dn;
-(2n+7)求dn;
查看答案和解析>>
科目: 来源: 题型:
已知函 数f(x)=logax(a>0且a≠1),若数列:2,f(a1),f(2),…,f(an),2n+4(n∈N*)成等差数列。
数f(x)=logax(a>0且a≠1),若数列:2,f(a1),f(2),…,f(an),2n+4(n∈N*)成等差数列。
(1)求数列{an}的通项an;
(2)若0<a<1,数列{an}的前n项和为Sn,求 Sn;
Sn;
(3)若a=2,令bn=an·f(an),对任意n∈N*,都有bn>f-1(t),求实数t的取值范围。
查看答案和解析>>
科目: 来源: 题型:
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145
(1)求数列{an}的通项公式bn;
(2)设数列{an}的通项an=loga(1+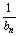 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与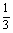 logabn+1的大小,并证明你的结论。
logabn+1的大小,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com