练习册

  • 练习册
  • 试题
    相关习题
     0  21638  21646  21652  21656  21662  21664  21668  21674  21676  21682  21688  21692  21694  21698  21704  21706  21712  21716  21718  21722  21724  21728  21730  21732  21733  21734  21736  21737  21738  21740  21742  21746  21748  21752  21754  21758  21764  21766  21772  21776  21778  21782  21788  21794  21796  21802  21806  21808  21814  21818  21824  21832  266669 

    科目： 来源：江西模拟 题型：单选题

    如图，∠C=90°，AC=BC，M，N分别为BC和AB的中点，沿直线MN将△BMN折起，使二面角B′-MN-B为60°，则斜线B'A与平面ABC所成角的正切值为（　　）
    A．
    		2
    5
    		B．
    		3
    5
    		C．
    4
    5
    		D．
    3
    5
    精英家教网

    查看答案和解析>>

    科目： 来源： 题型：

    观察（1）

    （2）

    由以上两式成立，推广到一般结论，写出你的推论。

    查看答案和解析>>

    科目： 来源：不详 题型：单选题

    在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，则D1O与平面ADD1A1所成的角的余弦值为（　　）
    A．
    		5
    5
    		B．
    		6
    6
    		C．
    		3
    2
    		D．
    		30
    6
    精英家教网

    查看答案和解析>>

    科目： 来源： 题型：

    （08年龙岩一中冲刺文）（12分）

    设函数，图像的一条对称轴是直线．

    （1）求；

    （2）求函数的单调增区间．

    查看答案和解析>>

    科目： 来源：河东区一模 题型：解答题

    如图所示四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，BC∥AD，PA=AB=BC=2，AD=4，E为PD的中点，F为PC中点．
    （Ⅰ）求证：CD⊥平面PAC；
    （Ⅱ）求证：BF∥平面ACE；
    （Ⅲ）求直线PD与平面PAC所成的角的正弦值．
    精英家教网

    查看答案和解析>>

    科目： 来源： 题型：

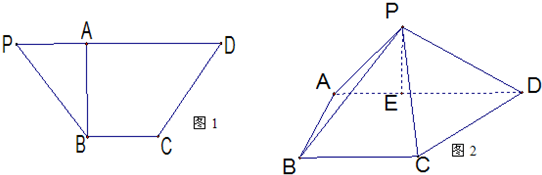
    （08年潍坊市二模）（12分）如图，正三棱锥P-ABC，PA＝4，AB＝2，D为BC中点，点E在AP上，满足AE＝3EP．

     

    　　（1）建立适当坐标系，写出A、B、D、E四点的坐标；

     

    　　（2）求异面直线AD与BE所成的角．

     

    查看答案和解析>>

    科目： 来源：不详 题型：解答题

    如图，三棱柱ABC-A1B1C1中，侧面AA1C1C⊥底面节ABCAA1=A1C=AC=2，AB=BC，且AB⊥BC，O为AC的中点．
    （I）求证：A1O⊥平面ABC；
    （Ⅱ）若E为BC1的中点，求证：OE∥平面A1AB；
    （III）求直线A1C与平面A1AB所成角的正弦值．
    精英家教网

    查看答案和解析>>

    科目： 来源：不详 题型：解答题

    如图（图1）等腰梯形PBCD，A为PD上一点，且AB⊥PD，AB=BC，AD=2BC，沿着AB折叠使得二面角P-AB-D为60°的二面角，连接PC、PD，在AD上取一点E使得3AE=ED，连接PE得到如图（图2）的一个几何体．
    精英家教网

    （1）求证：平面PAB⊥平面PCD；
    （2）求PE与平面PBC所成角的正弦值．

    查看答案和解析>>

    科目： 来源：韶关二模 题型：解答题


    精英家教网
    如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
    （1）求证：DC⊥平面ABC；
    （2）求BF与平面ABC所成角的正弦；
    （3）求二面角B-EF-A的余弦．
    精英家教网

    查看答案和解析>>

    科目： 来源： 题型：

    （08年龙岩一中冲刺文）（12分）

    据报道太空中有数以万计的失控的人造天体，被称为太空垃圾。假设若干年后有甲、乙两名太空保洁员可以用某种武器来清除太空垃圾．若甲、乙两名太空保洁员发射武器的命中率分别为、，若某次执行任务每人发射次．

    （1）求两人都恰好击中两个目标的概率；

    （2）求甲恰好比乙多击中一个目标的概率．

    查看答案和解析>>

    同步练习册答案