
科目: 来源: 题型:
已知函数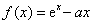 (e为自然对数的底数).
(e为自然对数的底数).
(Ⅰ)讨论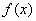 的单调性;
的单调性;
(Ⅱ)定义:函数 的定义域为
的定义域为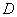 ,若
,若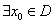 ,使
,使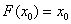 成立,则称
成立,则称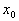 为
为 的不动点.
的不动点.
当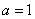 时,
时,
(ⅰ)证明:函数 存在唯一的不动点
存在唯一的不动点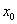 ,且
,且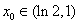 ;
;
(ⅱ)已知数列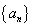 满足
满足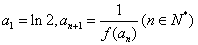 ,
,
求证: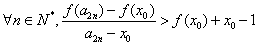 ,(其中
,(其中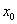 为
为 的不动点).
的不动点).
查看答案和解析>>
科目: 来源: 题型:
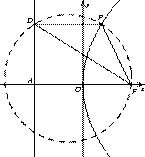
如图,抛物线E: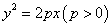 的焦点为
的焦点为 ,其准线
,其准线 与
与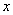 轴交于点
轴交于点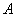 ,过抛物线E上的动点
,过抛物线E上的动点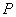 作
作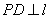 于点
于点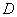 .当
.当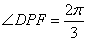 时,
时, 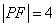 .
.
(Ⅰ)求抛物线E的方程;
(Ⅱ)过点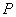 作直线
作直线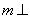
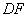 ,求直线
,求直线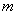 与抛物线E的交点个数;
与抛物线E的交点个数;
(Ⅲ)点C是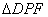 的外心,是否存在点
的外心,是否存在点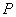 ,使得
,使得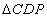 的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.
的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
某茶厂现有三块茶园,每块茶园的茶叶估值为6万元.根据以往经验:今年5月12日至14日是采茶的最佳时间,在此期间,若遇到下雨,当天茶园的茶叶估值减少为前一天的一半.现有两种采摘方案:
方案①:茶厂不额外聘请工人,一天采摘一块茶园的茶叶;
方案②:茶厂额外聘请工人,在12日采摘完全部茶叶,额外聘请工人的成本为3.2万元.
根据天气预报,该地区5月12日不降雨,13日和14日这两天降雨的概率均为40%.每天是否下雨不相互影响.
(Ⅰ)若采用方案①,求茶厂14日当天采茶的预期收益;
(Ⅱ)从统计学的角度分析,茶厂采用哪种方案更合理.
查看答案和解析>>
科目: 来源: 题型:
如图,梯形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在线段BC,AD上,EF∥AB.将四边形ABEF沿EF折起,连接AD,AC.
(Ⅰ)若BE=3,在线段AD上一点取一点P,使 ,求证:CP∥平面ABEF;
,求证:CP∥平面ABEF;
(Ⅱ)若平面ABEF⊥平面EFDC,且线段FA,FC,FD的长成等比数列,求二面角E-AC-F的大小.
 |
查看答案和解析>>
科目: 来源: 题型:
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为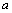 的平行线,将一根长度为
的平行线,将一根长度为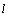 的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率
的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率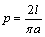 (
(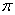 为圆周率).
为圆周率).
已知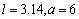 ,
,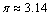 ,现随机掷14根相同的针(长度为
,现随机掷14根相同的针(长度为 )在这个平面上,记这些针与平行线(间距为
)在这个平面上,记这些针与平行线(间距为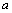 )相交的根数为
)相交的根数为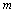 ,其相应的概率为
,其相应的概率为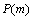 .当
.当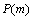 取得最大值时,
取得最大值时,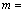 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com