
科目: 来源:广东省模拟题 题型:解答题
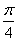 的角时,线段A1F与FA的比。
的角时,线段A1F与FA的比。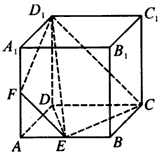
查看答案和解析>>
科目: 来源:同步题 题型:单选题
查看答案和解析>>
科目: 来源:东城区一模 题型:解答题
| 1 |
| 2 |
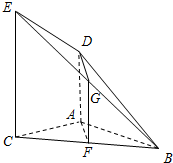
查看答案和解析>>
科目: 来源:海南省模拟题 题型:解答题

查看答案和解析>>
科目: 来源:湖南省高考真题 题型:单选题
[ ]
查看答案和解析>>
科目: 来源: 题型:
(08年莆田四中一模理) (14分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,若函数
,若函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“反数列”。
的“反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的反数列为
的反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)对(1)中![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)设![]() ,若数列
,若数列![]() 的反数列为
的反数列为![]() ,
,![]() 与
与![]() 的公共项组成的数列为
的公共项组成的数列为![]() ;求数列
;求数列![]() 前
前![]() 项和
项和![]()
查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:汕头二模 题型:解答题

查看答案和解析>>
科目: 来源:茂名一模 题型:解答题
| 1 |
| 2 |
| 2 |
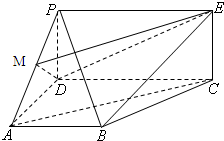
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com