练习册

  • 练习册
  • 试题
    相关习题
     0  237911  237919  237925  237929  237935  237937  237941  237947  237949  237955  237961  237965  237967  237971  237977  237979  237985  237989  237991  237995  237997  238001  238003  238005  238006  238007  238009  238010  238011  238013  238015  238019  238021  238025  238027  238031  238037  238039  238045  238049  238051  238055  238061  238067  238069  238075  238079  238081  238087  238091  238097  238105  266669 

    科目： 来源： 题型：选择题

    2．已知双曲线M的实轴长为2，且它的一条渐近线方程为y=2x，则双曲线M的标准方程可能是（　　）
    A．x2-4y2=1B．$\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1C．$\frac{{y}^{2}}{4}$-x2=1D．y2-4x2=1

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．中国古代数学名著《九章算术》中记载：今有大夫、不更、簪襃、上造、公士凡五人，共猜得五鹿，欲以爵次分之，问各得几何？意思是：今有大夫、不更、簪襃、上造、公士凡五人，他们共猎获5只鹿，欲按其爵级高低依次递减相同的量来分配，问各得多少，若五只鹿的鹿肉共500斤，则不更、簪襃、上造这三人共分得鹿肉斤数为（　　）
    A．200B．300C．$\frac{500}{3}$D．400

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．已知复数z=$\frac{2-i}{1+i}$（其中i为虚数单位），则|z|=（　　）
    A．$\frac{\sqrt{5}}{2}$B．$\frac{\sqrt{10}}{2}$C．$\frac{3\sqrt{2}}{2}$D．$\sqrt{10}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    19．已知集合A={x|y=$\sqrt{2-x}$}，B={x|3x-x2≥0}，则集合A∩B=（　　）
    A．[0，2]B．[0，3]C．[0，2）D．（-∞，0]

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．在直角坐标系xOy中，过点P（2，1）的直线l的参数方程为$\left\{\begin{array}{l}{x=2+\sqrt{3}t}\\{y=1+t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ=2cosθ，已知直线l与曲线C交于A、B两点．
    （1）求曲线C的直角坐标方程；
    （2）求|PA|•|PB|的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知函数f（x）=alnx+$\frac{1-{x}^{2}}{{x}^{2}}$，a∈R．
    （1）若f（x）的最小值为0，求实数a的值；
    （2）证明：当a=2时，f（x）≤f′（x）在x∈[1，2]上恒成立，其中f′（x）表示f（x）的导函数．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．在平面直角坐标系xOy中，双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-y2=1（a＞0）的左右焦点分别为F1、F2，离心率为$\frac{2\sqrt{3}}{3}$，且经过右焦点F2的直线l与双曲线的右支交于A、B两点．
    （1）求双曲线E的方程；
    （2）求△ABF1的面积的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

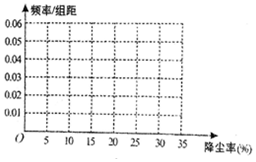    15．空气质量问题，全民关注，有需求就有研究，某科研团队根据工地常用高压水枪除尘原理，制造了雾霾神器----雾炮，虽然雾炮不能彻底解决问题，但是能在一定程度上起到防霾、降尘的作用，经过100次测试得到雾炮降尘率的频数分布表：
     降尘率（%）分组[0，5）[5，10）[10，15）[15，20）[20，25）[25，30）[30，35]
     频数 1015  1025  2015  5
    （1）在答题卡上作出这些数据的频率分布直方图；
    （2）估计雾炮降尘率的平均数；
    （3）若降尘率达到18%以上，则认定雾炮除尘有效，根据以上数据估计雾炮除尘有效的概率．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知数列{an}的前n项和为Sn，且对任意正整数n，都有3an=2Sn+3成立．
    （1）求数列{an}的通项公式；
    （2）设bn=log3an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．在△ABC中，∠BAC=90°，AB=3，AC=4，若点D、E都在边BC上，且∠BAD=∠CAE=15°，则$\frac{BD•BE}{CD•CE}$=$\frac{9}{16}$．

    查看答案和解析>>

    同步练习册答案