13．从1，2，3，4，5，6，7这七个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是$\frac{19}{35}$．

12．已知函数$f（x）=\left\{{\begin{array}{l}{2x-xlnx（x＞0）}\\{-{x^2}-\frac{3}{2}x（x≤0）}\end{array}}\right.$有且仅有四个不同的点关于直线y=1的对称点在直线kx+y-1=0上，则实数k的取值范围为（　　）

A．

$（\frac{1}{2}，1）$

B．

$（\frac{1}{2}，\frac{3}{4}）$

C．

$（\frac{1}{3}，1）$

D．

$（\frac{1}{2}，2）$

11．已知点F₁，F₂分别是双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左右两焦点，过点F₁的直线l与双曲线的左右两支分别交于P，Q两点，若△PQF₂是以∠PQF₂为顶角的等腰三角形，其中$∠PQ{F_2}∈[\frac{π}{3}，π）$，则双曲线离心率e
的取值范围为（　　）

A．

$[\sqrt{7}，3）$

B．

$[1，\sqrt{7}）$

C．

$[\sqrt{5}，3）$

D．

$[\sqrt{5}，\sqrt{7}）$

10．将函数$y=2sin（\frac{2}{3}x+\frac{3π}{4}）$图象上所有点的横坐标缩短为原来的$\frac{1}{3}$，纵坐标不变，再向右平移$\frac{π}{8}$个单位长度，得到函数y=g（x）的图象，则下列说法正确的是（　　）

	A．	函数g（x）的一条对称轴是$x=\frac{π}{4}$		B．	函数g（x）的一个对称中心是$（\frac{π}{2}，0）$
	C．	函数g（x）的一条对称轴是$x=\frac{π}{2}$		D．	函数g（x）的一个对称中心是$（\frac{π}{8}，0）$

9．某厂家为了解广告宣传费与销售轿车台数之间的关系，得到如下统计数据表：

广告费用x（万元）	2	3	4	5	6
销售轿车y（台数）	3	4	6	10	12

根据数据表可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=2.4，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，据此模型预测广告费用为9万元时，销售轿车台数为（　　）

A．

17

B．

18

C．

19

D．

20

8．等差数列{a_n}的前n项和为S_n，且S₅=15，a₂=5，则公差d等于（　　）

A．

-3

B．

-2

C．

-1

D．

2

7．已知函数f（x）=mlnx+$\frac{1}{x}$+2x，x∈[2，e]．
（Ⅰ）若m=-1，求函数f（x）的单调区间；
（Ⅱ）若对任意的m∈[0，1]，关于x的不等式f（x）≤（n+2）x恒成立，求实数n的取值范围．

6．每年的4月23日为世界读书日，为调查某高校学生（学生很多）的读书情况，随机抽取了男生，女生各20人组成的一个样本，对他们的年阅读量（单位：本）进行了统计，分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图．
男生年阅读量的频率分布表（年阅读量均在区间[0，60]内）：

本/年	[0，10）	[10，20）	[20，30）	[30，40）	[40，50）	[50，60]
频数	3	1	8	4	2	2

（Ⅰ）根据女生的频率分布直方图估计该校女生年阅读量的中位数；
（Ⅱ）在样本中，利用分层抽样的方法，从男生年与度量在[20，30），[30，40）的两组里抽取6人，再从这6人中随机抽取2人，求[30，40）这一组中至少有1人被抽中的概率；
（Ⅲ）若年阅读量不小于40本为阅读丰富，否则为阅读不丰富，依据上述样本研究阅读丰富与性别的关系，完成下列2×2列联表，并判断是否有99%的把握认为月底丰富与性别有关．

性别    阅读量	丰富	不丰富	合计
男
女
合计

P（K2≥k0）	0.025	0.010	0.005
k0	5.024	6.635	7.879

附：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

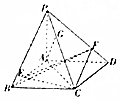5．已知四棱锥P-ABCD的底面ABCD是平行四边形，PA⊥平面ABCD，PA=AB=AC=2，AD=2$\sqrt{2}$，点E是线段AB上靠近B点的三等分点，点F、G分别在线段PD、PC上．
（Ⅰ）证明：CD⊥AG；
（Ⅱ）若三棱锥E-BCF的体积为$\frac{1}{6}$，求$\frac{FD}{PD}$的值．

4．已知在△ABC中，角A，B，C所对的边分别是a，b，c，且a、b、c成等比数列，c=$\sqrt{3}$bsinC-ccosB．
（Ⅰ）求B的大小；
（Ⅱ）若b=2$\sqrt{3}$，求△ABC的周长和面积．