
科目: 来源:月考题 题型:解答题
 、
、 、
、 ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响. 表示这三辆车中被堵的车辆数,求
表示这三辆车中被堵的车辆数,求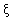 的分布列及数学期望E
的分布列及数学期望E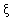 .
.查看答案和解析>>
科目: 来源:期末题 题型:解答题
 (0<a<1),三各射击一次,击中目标的次数记为X.
(0<a<1),三各射击一次,击中目标的次数记为X.查看答案和解析>>
科目: 来源:月考题 题型:解答题

 ,从该厂生产的产品中任取一件,其利润记为X,用这个样本的频率分布估计总体分布,将频率视为概率,求X的分布列和数学期望.
,从该厂生产的产品中任取一件,其利润记为X,用这个样本的频率分布估计总体分布,将频率视为概率,求X的分布列和数学期望.查看答案和解析>>
科目: 来源:期末题 题型:解答题

查看答案和解析>>
科目: 来源:高考真题 题型:解答题

查看答案和解析>>
科目: 来源:高考真题 题型:解答题
查看答案和解析>>
科目: 来源:期末题 题型:解答题



查看答案和解析>>
科目: 来源:高考真题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com