
科目: 来源:山东省月考题 题型:解答题
查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 、
、 、
、 、
、 、
、 、
、 。
。
 ,求ξ的数学期望。
,求ξ的数学期望。查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响。
,且各次投篮互不影响。查看答案和解析>>
科目: 来源:期末题 题型:解答题
 .且他们是否完成任务互不影响.
.且他们是否完成任务互不影响. ,设甲、乙、丙三人中能完成任务人数为X,求X的分布列和数学期望EX;(Ⅱ)若三人中只有丙完成了任务的概率为
,设甲、乙、丙三人中能完成任务人数为X,求X的分布列和数学期望EX;(Ⅱ)若三人中只有丙完成了任务的概率为 ,求p的值.
,求p的值.查看答案和解析>>
科目: 来源:期末题 题型:解答题
查看答案和解析>>
科目: 来源:月考题 题型:解答题
 .(I)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
.(I)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;查看答案和解析>>
科目: 来源:同步题 题型:解答题
查看答案和解析>>
科目: 来源:同步题 题型:解答题
查看答案和解析>>
科目: 来源:月考题 题型:解答题
查看答案和解析>>
科目: 来源:高考真题 题型:解答题
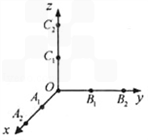
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com