科目： 来源：0103 期末题 题型：解答题

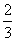有人预测：在2010年的广州亚运会上，排球赛决赛将在中国队与日本队之间展开，据以往统计， 中国队在每局比赛中胜日本队的概率为，比赛采取五局三胜制，即谁先胜三局谁就获胜，并停止比赛。
（1）求中国队以3：1获胜的概率；
（2）设ξ表示比赛的局数，求ξ的期望值。

科目： 来源：0103 期中题 题型：单选题

易建联在3月27日蓝网与活塞的比赛中，16投中12，保持此命中率不变，假设在下次比赛中有无限投篮权，那么他第一次投中时投篮次数的期望值为

[     ]

A、
B、1
C、
D、

科目： 来源：0103 期中题 题型：解答题

掷一枚质地不均匀的硬币连续掷3次，3次正面均朝上的概率为；
（1）抛掷这样的硬币3次，恰有1次正面向上的概率为多少？
（2）抛掷这样的硬币3次后，再抛掷一枚质地均匀的硬币1次，记四次抛掷后正面朝上的总次数为ξ，求随机变量ξ的分布列及期望Eξ。

科目： 来源：0110 期末题 题型：填空题

若的方差为3，则的方差为（    ）。

科目： 来源：0103 期末题 题型：填空题

随机变量ξ的分布列如下图所示，其中a，b，c成等差数列，若Eξ=，则Dξ的值是（    ）。

ξ -1 0 1 P a b c

科目： 来源：0103 期末题 题型：解答题

科目： 来源：0112 模拟题 题型：解答题

甲、乙、丙三人射击同一目标，各射击一次，已知甲击中目标的概率为，乙与丙击中目标的概率分别为m、n(m＞n)，每人是否击中目标是相互独立的，记目标被击中的次数为ξ，且ξ的分布列如下表：

ξ 0 1 2 3 P a b （Ⅰ）求m，n的值； （Ⅱ）求ξ的数学期望.

科目： 来源：0117 月考题 题型：解答题

某次国际象棋友谊赛在中国队和乌克兰队之间举行，比赛采用积分制，比赛规则规定赢一局得2分，平一局得1分，输一局得0分，根据以往战况，每局中国队赢的概率为，乌克兰队赢的概率为，且每局比赛输赢互不影响。若中国队第n局的得分记为a_n，令S_n=a₁+a₂+…+a_n。
（1）求S₃=4的概率；
（2）若规定：当其中一方的积分达到或超过4分时，比赛不再继续，否则，继续进行。设随机变量ξ表示此次比赛共进行的局数，求ξ的分布列及数学期望。

科目： 来源：福建省模拟题 题型：解答题

科目： 来源：江苏模拟题 题型：解答题

甲乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为，乙在每局中获胜的概率为，且各局胜负相互独立，求比赛停止时已打局数ξ的期望Eξ。