读下列程序，程序输出的函数y=．
INPUT  x
IF x＜0THENy=-x+1
ELSE
IF x=0THENy=0
ELSEy=x+1
END IF
END IF
PRINT y
END．

已知函数f（x）=2lnx-x²+ax，a∈R
（1）当a=2时，求函数f（x）的图象在x=1处的切线的方程；
（2）若函数f（x）-ax+m=0在[

1

e

，e}上有两个不等的实数根，求实数m的取值范围；
（3）若函数f（x）的图象与x轴交于不同的点A（x₁，0），B（x₂，0）且0＜x₁＜x₂，求证：f′（px₁+qx₂）＜0（其中实数p，q满足0＜p≤q，p+q=1）

已知向量

a

=（sinθ，cosθ-2sinθ），

b

=（1，2）
（1）若

a

⊥

b

，求tanθ的值；
（2）若

a

∥

b

，且θ为第Ⅲ象限角，求sinθ和cosθ的值．

已知A、B、C是直线l上的三点，向量

OA

、

OB

、

OC

满足：

OA

=[y+3xf′（1）]

OB

-2lnx•

OC

 则函数y=f（x）的表达式为．

函数y=

x2+mx+1

的值域是[0，+∞），则实数m的取值范围是．

已知

lim

x→∞

(

2x2

x+1

-ax-b)=4，其中a，b∈R，则

b

a

的值为（　　）

（1）若点A（a，b）（其中a≠b）在矩阵M=

0 -1 1 0

对应变换的作用下得到的点为B（-b，a）．
（Ⅰ）求矩阵M的逆矩阵；
（Ⅱ）求曲线C：x²+y²=1在矩阵N=

0 1 2 1 0

所对应变换的作用下得到的新的曲线C′的方程．
（2）选修4-4：坐标系与参数方程
（Ⅰ）以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的长度单位已知直线的极坐标方程为θ=

π

4

(ρ∈R)，它与曲线

x=2+ 5 cosθ y=1+ 5 sinθ

(θ为参数）相交于两点A和B，求|AB|；
（Ⅱ）已知极点与原点重合，极轴与x轴正半轴重合，若直线C₁的极坐标方程为：ρcos(θ-

π

4

)=

2

，曲线C₂的参数方程为：

x=1+cosθ y=3+sinθ

（θ为参数），试求曲线C₂关于直线C₁对称的曲线的直角坐标方程．
（3）选修4-5：不等式选讲
（Ⅰ）已知函数f（x）=|x+3|，g（x）=m-2|x-11|，若2f（x）≥g（x+4）恒成立，求实数m的取值范围．
（Ⅱ）已知实数x、y、z满足2x²+3y²+6z²=a（a＞0），且x+y+z的最大值是1，求a的值．

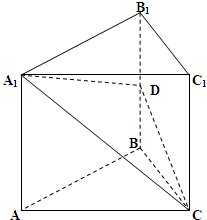如图，在直三棱柱ABC-A₁B₁C₁中，底面△ABC为等腰直角三角形，∠B=90°，D为棱BB₁上一点，且面DA₁ C⊥面AA₁C₁C．
（1）求证：D为棱BB₁中点；
（2）

AA1

AB

为何值时，二面角A-A₁D-C的平面角为60°．

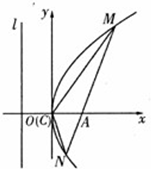如图，某旅游区拟在公路l（南北向）旁开发一个抛物线形的人工湖，湖沿岸上每一点到公路l的距离与到A处的距离相等，并在湖中建造一个三角形的游乐区MNC，三个顶点M，N，C都在湖沿岸上，直线通道MN经过A处．经测算，A在公路l正东方向200米处，C在A的正西方向100米处，现以点C为坐标原点，以线段CA所在直线为x轴建立平面直角坐标系．
（1）求抛物线的方程；
（2）试确定直线通道MN的位置，使得三角形游乐区MNC的面积最小，并求出最小值．