练习册

  • 练习册
  • 试题
    相关习题
     0  45718  45726  45732  45736  45742  45744  45748  45754  45756  45762  45768  45772  45774  45778  45784  45786  45792  45796  45798  45802  45804  45808  45810  45812  45813  45814  45816  45817  45818  45820  45822  45826  45828  45832  45834  45838  45844  45846  45852  45856  45858  45862  45868  45874  45876  45882  45886  45888  45894  45898  45904  45912  266669 

    科目： 来源： 题型：

    （2012•浦东新区一模）定义数列{xn}，如果存在常数p，使对任意正整数n，总有（xn+1-p）（xn-p）＜0成立，那么我们称数列{xn}为“p-摆动数列”．
    （1）设an=2n-1，bn=(-
    12
    )n    ，n∈N*，判断{an}、{bn}是否为“p-摆动数列”，并说明理由；
    （2）设数列{cn}为“p-摆动数列”，c1＞p，求证：对任意正整数m，n∈N*，总有c2n＜c2m-1成立；
    （3）设数列{dn}的前n项和为Sn，且Sn=(-1)n•n，试问：数列{dn}是否为“p-摆动数列”，若是，求出p的取值范围；若不是，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

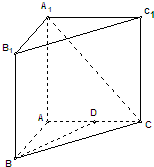    （2012•浦东新区一模）如图，直三棱柱ABC-A1B1C1中，AB=AC=AA1=2，∠ABC=45°．
    （1）求直三棱柱ABC-A1B1C1的体积；
    （2）若D是AC的中点，求异面直线BD与A1C所成的角．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•浦东新区一模）1，2，3，4，5共有5!种排列a1，a2，a3，a4，a5，其中满足“对所有k=1，2，3，4，5都有ak≥k-2”的不同排列有
    54
    54
    种．

    查看答案和解析>>

    科目： 来源： 题型：

    甲乙两个盒子中装有大小相同的小球，甲盒中有2个黑球和2个红球，乙盒中有2个黑球和3个红球，从甲乙两盒中各任取一球交换.

       （1）求交换后甲盒中恰有2个黑球的概率；

       （2）求交换后甲盒中的黑球数没有减少的概率.

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•浦东新区一模）非零向量
    OA
    与
    OB
    ，对于任意的t∈R，| 
    OA
    +t
    OB
     |    的最小值的几何意义为
    点A到直线OB的距离
    点A到直线OB的距离
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•揭阳一模）一般来说，一个人脚掌越长，他的身高就越高．现对10名成年人的脚掌长x与身高y进行测量，得到数据（单位均为cm）作为一个样本如上表示．
    脚掌长（x） 20 21 22 23 24 25 26 27 28 29
    身高（y） 141 146 154 160 169 176 181 188 197 203
    （1）在上表数据中，以“脚掌长”为横坐标，“身高”为纵坐标，作出散点图后，发现散点在一条直线附近，试求“身高”与“脚掌长”之间的线性回归方程
    y
    =bx+a；
    （2）若某人的脚掌长为26.5cm，试估计此人的身高；
    （3）在样本中，从身高180cm以上的4人中随机抽取2人作进一步的分析，求所抽取的2人中至少有1人身高在190cm以上的概率．
    （参考数据：
    10
    i=1
    (xi-
    .
    x
    )(yi-
    .
    y
    )=577.5    ，
    10
    i=1
    (xi-
    .
    x
    )    2    =82.5    ）

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•揭阳一模）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足
    a
    sinA
    =
    c
    		3
    cosC
    ．
    （1）求角C的大小；
    （2）求
    		3
    sinA-cosB    的最大值，并求取得最大值时角A，B的大小．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•揭阳一模）如图所示，AB是⊙O的直径，过圆上一点E作切线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．若CB=2，CE=4，则⊙O 的半径长为
    3
    3
    ；AD的长为
    24
    5
    24
    5
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•揭阳一模）已知曲线C1：ρ=2和曲线C2：ρcos(θ+
    π
    4
    )=
    		2
    ，则C1上到C2的距离等于
    		2
    的点的个数为
    2
    2
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•揭阳一模）给出下列等式：
    		2
    =2cos
    π
    4
    ，
    		2+
    		2
    =2cos
    π
    8
    ，
    		2+
    		2+
    		2
    =2cos
    π
    16
    ，…请从中归纳出第n个等式：
    		2+…+
    		2+
    		2
    n个2
    =
    2cos
    π
    2n+1
    2cos
    π
    2n+1
    ．

    查看答案和解析>>

    同步练习册答案