练习册

  • 练习册
  • 试题
    相关习题
     0  46303  46311  46317  46321  46327  46329  46333  46339  46341  46347  46353  46357  46359  46363  46369  46371  46377  46381  46383  46387  46389  46393  46395  46397  46398  46399  46401  46402  46403  46405  46407  46411  46413  46417  46419  46423  46429  46431  46437  46441  46443  46447  46453  46459  46461  46467  46471  46473  46479  46483  46489  46497  266669 

    科目： 来源： 题型：

    设圆C：（x-3）2+y2=4经过抛物线y2=2px（p＞0）的焦点，则抛物线的方程是
    y2=20x或y2=4x
    y2=20x或y2=4x
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    对于函数f（x）=x|x|+px+q现给出四个命题，其中所有正确的命题序号是（　　）
    ①q=0时，f（x）为奇函数；             
    ②y=f（x）的图象关于（0，q）对称；
    ③p=0，q＞0，f（x）有且只有一个零点；  
    ④f（x）至多有2个零点．

    查看答案和解析>>

    科目： 来源： 题型：

    记全集U={1，2，3，4，5，6，7，8}，A={1，2，3，5}，B={2，4，6}则图中阴影部分所表示的集合是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    已知直线l：x=my+1过椭圆C：
    x2
    a2
    +
    y2
    b2
    =1    的右焦点F，抛物线x2=4
    		3
    y    的焦点为椭圆C的上顶点，且直线l交椭圆C于A，B两点，点A，F，B在直线x=4上的射影依次为点D，K，E．
    （1）求椭圆C的方程；
    （2）若直线l交y轴于点M，且
    MA
    =λ1
    AF
    ，
    MB
    =λ2
    BF
    ，当m变化时，证明：λ1+λ2=-
    8
    3
    ；
    （3）连接AE，BD，试探索当m变化时，直线AE与BD是否相交于定点？若是，求出定点的坐标，并给出证明；否则，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    某高速公路指挥部接到通知，24小时后将有一场超历史记录的大暴雨，为确保万无一失，指挥部决定在24小时内筑一道临时堤坝，以防山洪淹没正在紧张施工的隧道工程。经测算，除现有施工人员外，还须调用翻斗车搬运立方米的土方。已知每辆翻斗车每小时可搬运的土方量为，指挥部可调用25辆上述型号的翻斗车，但其中只有一辆可以立即投入施工，其余车辆需要从各处紧急抽调，每隔20分钟有一辆车到达并投入施工。

    （1）从第一辆车投入施工算起，第25辆车须多久才能到达？

    （2）24小时内能否完成防洪堤坝工程？请说明理由。

    查看答案和解析>>

    科目： 来源： 题型：

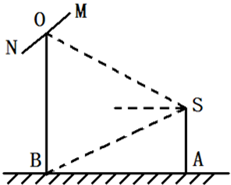    如图，摄影爱好者S在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为30°，已知S的身高约为
    		3
    米（将眼睛距地面的距离SA按
    		3
    米处理）．
    （1）求摄影者到立柱的水平距离AB和立柱的高度OB；
    （2）立柱的顶端有一长为2米的彩杆MN，且MN绕其中点O在S与立柱所在的平面内旋转．在彩杆转动的任意时刻，摄影者观察彩杆MN的视角∠MSN（设为θ）是否存在最大值？若存在，请求出∠MSN取最大值时cosθ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    等差数列{an}满足3a5=5a8，Sn是数列{an}的前n项和．
    （1）若a1=1，当Sn取得最大值时，求n的值；
    （2）若a1=-46，记bn=
    Sn-ann
    ，求bn的最小值．

    查看答案和解析>>

    科目： 来源： 题型：

    一个房间有4扇同样的窗子，其中只有一扇窗子是打开的．房间里一只燕子只能从开着的窗子飞出去，燕子在房子里一次又一次地向着窗户飞去，试图飞出房间．假定燕子飞向各扇窗子是等可能的．
    （1）假定燕子是没有记忆的，求它恰好在第2次试飞时出了房间的概率；
    （2）假定这只燕子是有记忆的，它飞向任一窗子的尝试不多于一次，若这只燕子恰好在第η次试飞时飞出了房间，求试飞次数η的分布列及其数学期望．

    查看答案和解析>>

    科目： 来源： 题型：

    在（x-3）5的展开式中，含x3的项的系数等于
    90
    90
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•蓝山县模拟）如图，AB是⊙O的直径，直线DE切⊙O于点D，且与AB的延长线交于点C，若CD=
    		3
    ，CB=1，则∠ACE=
    30°
    30°
    ．

    查看答案和解析>>

    同步练习册答案