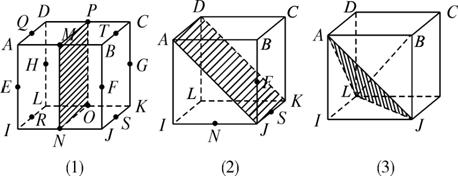
(1)试举出一直线与一平面相互垂直的例子(不少于4例)；

(2)若一直线与一平面相互垂直，我们就说这条直线与这个平面构成了一个“垂直关系组”，两个“垂直关系组”当且仅当其中两条直线和两个平面不全同一时称为相异的(或不同的).试求与正方体的棱相关的“垂直关系组”的个数.

(1)求证AC⊥BC₁;

(2)求证AC₁∥平面CDB₁；

(3)求异面直线AC₁与B₁C所成角的余弦值.

A.4条              B.6条               C.8条                 D.12条

①垂直于同一直线的两条直线互相平行.

②垂直于同一平面的两个平面互相平行.

③若直线l₁,l₂与同一平面所成的角相等，则l₁,l₂互相平行.

④若直线l₁,l₂是异面直线，则与l₁,l₂都相交的两条直线是异面直线.

其中假命题的个数是(    )

A.1                B.2                  C.3                   D.4

①若m⊥α,m⊥β,则α∥β;

②若α⊥γ,β⊥γ,则α∥β;

③若mα,nβ,m∥n,则α∥β;

④若m、n是异面直线，mα,m∥β,nβ,n∥α,则α∥β.

其中真命题是(    )

A.①和②             B.①和③            C.③和④             D.①和④