①f(x)在D上是单调函数;

②存在闭区间［a,b］?D,使f(x)在区间［a,b］上的值域也是［a,b］.

那么就称函数y=f(x)为闭函数.

试判断函数y=x²+2x〔x∈［-1,+∞)〕是否为闭函数,如果是闭函数,那么求出符合条件的区间［a,b］；如果不是闭函数,请说明理由.

A.a≤2                B.a＜2                 C.0＜a＜2             D.a＜2，且a≠0

f(t)=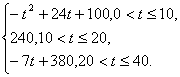

(1)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(2)讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？

(3)一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？

(1)写出y关于x的函数关系式，并求出定义域；

(2)求鱼群的年增长量的最大值；

(3)当鱼群的年增长量可达到最大值时，求k所应满足的条件.

(1)f(x)的最小值g(t)的解析式；

(2)求g(t)的最小值.

A.m≤3                 B.m≥3                  C.m≤-3                D.m≥-3