A.(-∞,0)         B.(-∞,-1)         C.［0,+∞)         D.［-1,+∞)

Wish you success,分组为Wi,sh,yo,us,uc,ce,ss得到

其中英文的a,b,c,…,z的26个字母(不论大小写）依次对应1，2，3，…,26这26个自然数，见表格:

给出如下一个变换公式,将明文转换为密文.如

→→，即ce变成mc(说明:29÷26余数为3）.

又如→→,即wi变成oa(说明:41÷26余数为15，105÷26余数为1）.

(1）按上述方法将明文star译成密文；

(2)若按上述方法将某明文译成的密文是kcwi，请你找出它的明文.

(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式；

(2)为使本年度的年利润比上年有所增加，问投入成本增加的比例x应在什么范围内?

(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?

(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;

(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)

(1)多少小时后蓄水池中水量最少?

(2)若蓄水池中存水量少于150吨时,就会出现供水紧张现象,问有几小时供水紧张?

(1)写出g(x)、h(x)的解析式；

(2)比较g(x)与h(x)的大小，并写出这216名工人完成总任务的时间f(x)的解析式；

(3)应怎样分组，才能使完成总任务用的时间最少？

A.①②               B.②③               C.③④               D.①④

A.2                      B.4                   C.6                   D.8

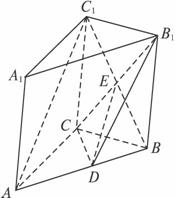
(1)求证：AC₁//平面CDB₁；

(2)求B₁到平面A₁BC₁的距离.

(1)在该时段内，当汽车的平均速度v为多少时，车流量最大？最大车流量为多少？(精确到0.1千辆/时)

(2)若要求在该时段内车流量超过10千辆/时，则汽车的平均速度应在什么范围内？