设全集U={1,2,3,4,5,6},集合P={3,4},集合Q={1,3,6},则P∩Q等于A.{1,3,4,6} B.{2,5} C.{3} D.{4}——青夏教育精英家教网—

相关习题

0 56957 56965 56971 56975 56981 56983 56987 56993 56995 57001 57007 57011 57013 57017 57023 57025 57031 57035 57037 57041 57043 57047 57049 57051 57052 57053 57055 57056 57057 57059 57061 57065 57067 57071 57073 57077 57083 57085 57091 57095 57097 57101 57107 57113 57115 57121 57125 57127 57133 57137 57143 57151 266669

科目： 来源： 题型：

设全集U={1,2,3,4,5,6},集合P={3,4},集合Q={1,3,6},则P∩

Q等于

A.{1,3,4,6} B.{2,5} C.{3} D.{4}

查看答案和解析>>

科目： 来源： 题型：

(1)已知抛物线y²=2px(p＞0),过焦点F的动直线l交抛物线于A、B两点,O为坐标原点,求证:·为定值;

(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A、B两点,存在定点P,使得PA·PB为定值.请写出关于椭圆的类似结论,并给出证明.

查看答案和解析>>

科目： 来源： 题型：

已知函数f(x)=2+.数列{a_n}中,a₁=a,a_n+1=f(a_n)(n∈N^*).当a取不同的值时,得到不同的数列{a_n},如当a=1时,得到无穷数列1,3,,,…;当a=-时,得到有穷数列-,0.

(1)求a的值,使得a₃=0;

(2)设数列{b_n}满足b₁=-,b_n=f(b_n+1)(n∈N^*),求证:不论a取{b_n}中的任何数,都可以得到一个有穷数列{a_n};

(3)求a的取值范围,使得当n≥2时,都有＜a_n＜3.

查看答案和解析>>

科目： 来源： 题型：

已知函数f(x)=x³-x²-3x+,直线l:9x+2y+c=0.

(1)求证:直线l与函数y=f(x)的图象不相切;

(2)若当x∈［-2,2］时,函数y=f(x)的图象在直线l的下方,求c的范围.

查看答案和解析>>

科目： 来源： 题型：

如图,在正方体ABCD—A₁B₁C₁D₁中,E为AB的中点.

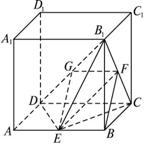
(1)求AD和B₁C所成的角;

(2)证明平面EB₁D⊥平面B₁CD;

(3)求二面角EB₁CD的大小(用反三角函数表示).

查看答案和解析>>

科目： 来源： 题型：

某学校对学生身高进行统计.所有学生的身高数近似服从正态分布N(160，25)，已知所有学生中身高在153cm以下的人数为202人，则该校学生总人数约为__________人(用整数作答)

以下供查阅的部分标准正态分布数据可选择使用：

x₀	1.3	1.4	1.9	2.0	2.1
φ(x₀)=P(x＞x₀)	0.9032	0.9192	0.9713	0.9772	0.9821

查看答案和解析>>

科目： 来源： 题型：

正四棱锥P-ABCD的底面边长为2，侧棱长为,－且它的五个顶点都在同一球面上，则此球的表面积为_________.

查看答案和解析>>

科目： 来源： 题型：

设F为抛物线y=x²的焦点，与抛物线相切于点P(-4，-4)的直线l与x轴的交点为Q，则∠PQF=______________.

查看答案和解析>>

科目： 来源： 题型：

若(ax-)⁵的展开式中x³的系数是-80，则正实数a的值是____________.

查看答案和解析>>

科目： 来源： 题型：

一位学生每天骑自行车上学,从他家到学校共有5个交通岗,假设他在每个交通岗遇到红灯是相互独立的,且首末两个交通岗遇到红灯的概率均为p,其余3个交通岗遇到红灯的概率均为.

(1)若p=,求该学生在第三个交通岗第一次遇到红灯的概率;

(2)若该学生至多遇到一次红灯的概率不超过,求p的取值范围.

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学