
科目: 来源: 题型:
(1)分别求出方案甲以及c=0.95时方案乙的用水量,并比较哪一种方案用水量较少;
(2)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论a取不同数值时对最少总用水量多少的影响.
查看答案和解析>>
科目: 来源: 题型:
(1)若x=a+(t2-3)b与y=-ka+tb垂直,求k关于t的函数关系式k=f(t);
(2)试确定k=f(t)的单调区间.
查看答案和解析>>
科目: 来源: 题型:
A.(-4,0)∪(0,4) B.(-4,-1)∪(1,4)
C.(-2,-1)∪(1,2) D.(-4,-2)∪(2,4)
查看答案和解析>>
科目: 来源: 题型:
(Ⅰ)求函数f(x)在区间[1,e]上的最大值和最小值;
(Ⅱ)求证:在区间(1,+∞)上函数f(x)的图象在函数g(x)=![]() x3的图象的下方;
x3的图象的下方;
(Ⅲ)设h(x)=f′(x),证明:[h(x)]n-h(xn)≥2n-2.
查看答案和解析>>
科目: 来源: 题型:
(1)若函数f(x)=![]() 的图象上有两个关于原点对称的不动点,求a、b满足的条件;
的图象上有两个关于原点对称的不动点,求a、b满足的条件;
(2)在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A、A′,P为函数f(x)的图象上的另一点,且其纵坐标yP>3,求点P到直线AA′距离的最小值及取得最小值时点P的坐标.
(3)命题“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,试给予证明,并举出一例;若不正确,试举一反例说明.
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示.
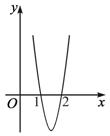
求:(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
查看答案和解析>>
科目: 来源: 题型:
A.(-∞,1) B.(0,1) C.(1,+∞) D.[1,+∞)
查看答案和解析>>
科目: 来源: 题型:
(1)对满足-1≤a≤1的一切a的值,都有g(x)<0,求实数x的取值范围;
(2)设a=-m2,当实数m在什么范围内变化时,函数y=f(x)的图象与直线y=3只有一个公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com