练习册

  • 练习册
  • 试题
    相关习题
     0  57100  57108  57114  57118  57124  57126  57130  57136  57138  57144  57150  57154  57156  57160  57166  57168  57174  57178  57180  57184  57186  57190  57192  57194  57195  57196  57198  57199  57200  57202  57204  57208  57210  57214  57216  57220  57226  57228  57234  57238  57240  57244  57250  57256  57258  57264  57268  57270  57276  57280  57286  57294  266669 

    科目： 来源： 题型：

    如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的，其中AB=4，BC=2，CC1=3，BE=1.

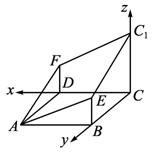
    (1)求BF与平面BCC1E所成的角；

    (2)求截面AEC1F与平面ABCD所成二面角的大小；

    (3)在线段CC1上是否存在一点C2，使C2在平面AEC1F上的射影恰为△EC1F的重心.

    查看答案和解析>>

    科目： 来源： 题型：

    如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1.已知AB=,BB1=2,BC=1,∠BCC1=,求:

    (1)异面直线AB与EB1的距离;

    (2)二面角A—EB1—A1的平面角的正切值.

    查看答案和解析>>

    科目： 来源： 题型：

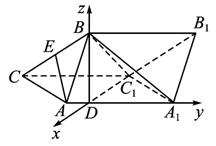
    如图，斜三棱柱ABC—A1B1C1的侧面AA1C1C的面积为的菱形，∠ACC1为锐角，侧面ABB1A1⊥侧面AA1C1C，且A1B=AB=AC=1.

    (1)求证AA1⊥BC1；

    (2)求A1B1平面ABC的距离.

    查看答案和解析>>

    科目： 来源： 题型：

    在空间直角坐标系中，已知A（2，3，1），B（4，1，2），C（6，3，7），D（-5，-4，8），DH⊥平面ABC，垂足为H，直线DH交平面xOy于点M，则点M的坐标是（    ）

    A.（4，7，0）        B.（7，4，0）          C.（-4，7，0）       D.（-7，-4，0）

    查看答案和解析>>

    科目： 来源： 题型：

    正方体ABCD—A1B1C1D1的棱长为1，以D为原点，、、所在直线为x、y、z轴建立直角坐标系D—xyz,且MN是AB1与BC1的公垂线，M在AB1上，N在BC1上，则等于（    ）

    A.（1，，）                           B.（，1，）

    C.（-，，-）                       D.（，-，）

    查看答案和解析>>

    科目： 来源： 题型：

    如图,已知长方体ABCD—A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.

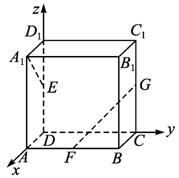
    (1)求异面直线AE与BF所成的角;

    (2)求平面BDF与平面AA1B所成二面角(锐角)的大小;

    (3)求点A到平面BDF的距离.

    查看答案和解析>>

    科目： 来源： 题型：

    如图,长方体ABCD—A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是（    ）

    A.arccos           B.            C.arccos            D.

    查看答案和解析>>

    科目： 来源： 题型：

    如下图所示，在矩形ABCD中，AB=1，BC=a,PA⊥平面ABCD，PA=1.

    （1）在BC边上是否存在点Q，使得PQ⊥QD？说明理由.

    （2）若BC边上有且仅有一个点Q，使PQ⊥QD，求AD与平面PDQ所成角的正弦值.

    （3）在（2）的条件下，能求出平面PQD与平面PAB所成的角的大小吗？

    查看答案和解析>>

    科目： 来源： 题型：

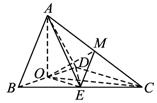
    如图，四面体ABCD中，O、E分别是BD、BC的中点，CA=CB=CD=BD=2,AB=AD=.

    (Ⅰ)求证：AO⊥平面BCD；

    (Ⅱ)求异面直线AB与CD所成角的大小；

    (Ⅲ)求点E到平面ACD的距离.

    查看答案和解析>>

    科目： 来源： 题型：

    已知椭圆C：+y2=1的两个焦点为F1、F2，若C上总存在点P，使得∠F1PF2=120°，则m的范围可以是

    A.m∈(1,2)∪(2,3)                                  B.m∈(-∞,1)∪(3,+∞)

    C.m∈(-∞,-2］∪［，2)∪(2,］∪［6，+∞)        D.m∈［］

    查看答案和解析>>

    同步练习册答案