
科目: 来源: 题型:
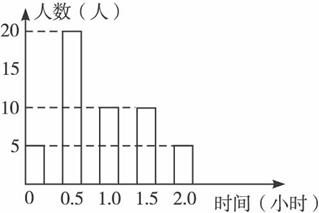
A.0.6小时 B.0.9小时 C.1.0小时 D.1.5小时
查看答案和解析>>
科目: 来源: 题型:
A.f(x)=|x|,g(x)=![]() B.f(x)=
B.f(x)=![]() ,g(x)=(
,g(x)=(![]() )2
)2
C.f(x)=![]() ,g(x)=x+1 D.f(x)=
,g(x)=x+1 D.f(x)=![]() g(x)=
g(x)=![]()
查看答案和解析>>
科目: 来源: 题型:
(1)求离心率e的取值范围.
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]() .
.
①求此时椭圆G的方程;
②(理)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,![]() )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
(文)设斜率为1的直线与椭圆G相交于不同的两点A、B,Q为AB的中点,点P的坐标为(0![]() ),若直线PQ垂直平分弦AB,求AB所在的直线方程.
),若直线PQ垂直平分弦AB,求AB所在的直线方程.
查看答案和解析>>
科目: 来源: 题型:
(1)试解释f(0)=10,g(0)=20的实际意义;
(2)设f(x)=![]() x+10,g(x)=
x+10,g(x)=![]() +20,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
查看答案和解析>>
科目: 来源: 题型:
(1)判断{![]() }是否为等差数列?并证明你的结论;
}是否为等差数列?并证明你的结论;
(2)求Sn和an;
(3)求证:S12+S22+…+Sn2≤![]()
![]() .
.
(文)数列{an}的前n项和Sn(n∈N*),点(an,Sn)在直线y=2x-3n上.
(1)求证:数列{an+3}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在成等差数列的三项?若存在,求出一组适合条件的三项;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
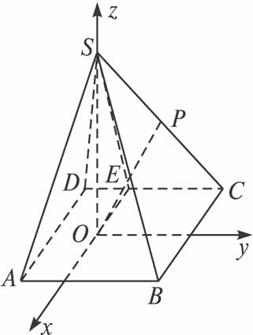
(1)求证:![]() 是定值.
是定值.
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
(文)如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
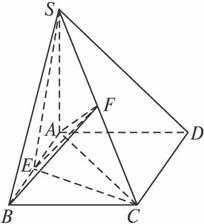
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com