
科目: 来源: 题型:
(1)求数列{an}的通项公式;
(2)证明:对一切正整数n,不等式a1·a2·…·an<2·n!恒成立.
查看答案和解析>>
科目: 来源: 题型:
21.如图,椭圆Q:![]() =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
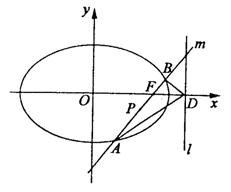
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
).确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
查看答案和解析>>
科目: 来源: 题型:
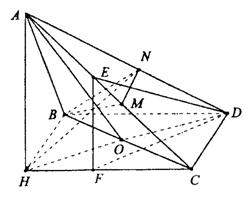
(1)求证:AD⊥BC;
(2)求二面角B-AC-D的大小;
(3)在线段AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定点E的位置;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
19.如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的
点,线段MN经过△ABC的中心G.设∠MGA=α(![]() ≤α≤
≤α≤![]() ).
).
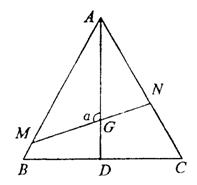
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为α的函数;
(2)求y=![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
18.某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出两个红球可获得奖金50元.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.令ξ表示甲、乙两人摸球后获得的奖金总额.求
(1)ξ的分布列; (2)ξ的数学期望.
查看答案和解析>>
科目: 来源: 题型:
17. 已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
16.已知圆M:(x+cosθ)2+(y-sin θ)2=1,直线l:y=kx,下面四个命题
(A)对任意实数k和θ,直线l和圆M相切;
(B)对任意实数k和θ,直线l和圆M有公共点;
(C)对任意实数θ,必存在实数k,使得直线l和圆M相切;
(D)对任意实数k,必存在实数θ,使得直线l和圆M相切.
其中真命题的代号是_________(写出所有真命题的代号).
查看答案和解析>>
科目: 来源: 题型:
15.如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1=![]() .P是BC1上一动点,则CP+PA1的最小值为_________.
.P是BC1上一动点,则CP+PA1的最小值为_________.
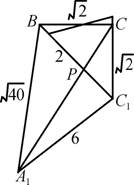
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com