f(t)=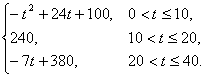

（1）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

（2）讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？

（3）一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？

(1)求横断面中有水面积S（米²）与水深h（米）的函数关系式；

(2)若S为15.4米²，则水渠的深度为多少米（按=1.4计算）时，渠道渗水量最小?（即水渠横断面与水接触部分的周界最小）

（1）把全程运输成本y（元）表示为速度v(千米/时)的函数，并指出这个函数的定义域；

（2）为了使全程运输成本最小，汽车应以多大速度行驶？

(1)证明定义在R上的二次函数f(x)=ax²+bx+c(a＜0)是凸函数;

(2)对于(1)中的二次函数f(x)=ax²+bx+c(a＜0),若|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,求|f(4)|取得最大值时函数y=f(x)的解析式.

A.（-12,-4]∪［4,+∞)                         B.［-12,-4)∪［4,+∞)

C.（-∞,-12）∪（-4,4）                      D.［-12,+∞）